
已知数列![]() 满足递推关系式:
满足递推关系式:![]() ,
,![]() .
.
(1)若![]() ,证明:(ⅰ)当
,证明:(ⅰ)当![]() 时,有
时,有![]() ;(ⅱ)当
;(ⅱ)当![]() 时,有
时,有![]() .
.
(2)若![]() ,证明:当
,证明:当![]() 时,有
时,有![]() .
.
证明略
因为![]() ,故
,故![]() ,即数列
,即数列![]() 为递增数列.
为递增数列.
(1)(ⅰ)由![]() 及
及![]() 可求得
可求得![]() ,于是当
,于是当![]() 时,
时,![]() ,于是
,于是![]() ,即当
,即当![]() 时,
时,![]() .
.
…………………………5分
(ⅱ)由于![]() 时,
时,![]() ,所以
,所以![]() 时,
时,![]() .
.
由![]() 可得
可得![]() .
.
先用数学归纳法证明下面的不等式成立:![]() (
(![]() ).
).
Ⅰ)当![]() 时,
时,![]() ,结论成立.
,结论成立.
Ⅱ)假设结论对![]() 成立,即
成立,即![]() ,则结合(ⅰ)的结论可得
,则结合(ⅰ)的结论可得
![]() ,即当
,即当![]() 时结论也成立.
时结论也成立.
综合Ⅰ),Ⅱ)可知,不等式![]() 对一切
对一切![]() 都成立.
都成立.
因此,当![]() 时,
时,![]()
![]() ,即
,即![]() .
.
又![]() ,
,![]() ,所以当
,所以当![]() 时,有
时,有![]() .
.
…………………………10分
(2)由于![]() ,而数列
,而数列![]() 为递增数列,故当
为递增数列,故当![]() 时,有
时,有![]() .
.
由![]() 可得
可得![]() ,而
,而![]() ,于是
,于是
![]() .
.
下面先证明:当![]() 时,有
时,有![]() (*)
(*)
Ⅰ)根据![]() 及
及![]() 计算易得
计算易得![]() ,
,
![]() ,而
,而![]() ,
,
故![]() ,即当
,即当![]() 时,结论成立.
时,结论成立.
Ⅱ)假设结论对![]() 成立,即
成立,即![]() .
.
因为![]() ,而函数
,而函数![]() 在
在![]() 时为增函数,所以
时为增函数,所以
![]() ,
,
即当![]() 时结论也成立.
时结论也成立.
综合Ⅰ),Ⅱ)可知,不等式![]() 对一切
对一切![]() 都成立.
都成立.
于是当![]() 时,
时,![]() ,故
,故![]() ,所以
,所以![]() .
.
…………………………20分


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:高中数学 来源: 题型:
2
| ||
| an+1 |
| 1 |
| a1+1 |
| 1 |
| a2+1 |
| 1 |
| an+1 |
| 1 |
| 2n |
查看答案和解析>>
科目:高中数学 来源:2010-2011学年湖北省武汉二中、龙泉中学高一下学期期末联考数学 题型:解答题
(14分)已知数列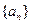 满足递推关系,
满足递推关系,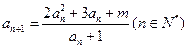 ,又
,又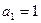
(1)当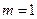 时,求
时,求 证数列
证数列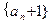 为等比数列;
为等比数列;


(2)当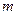 在什么范围内取值时,能使数列
在什么范围内取值时,能使数列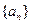 满足不等式
满足不等式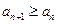 恒成立?
恒成立?
(3)当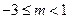 时,证明:
时,证明: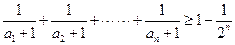 .
.
查看答案和解析>>
科目:高中数学 来源:2013届湖北省高一下学期期末联考数学 题型:解答题
(14分)已知数列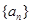 满足递推关系,
满足递推关系,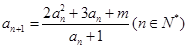 ,又
,又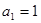
(1)当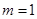 时,求证数列
时,求证数列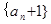 为等比数列;
为等比数列;

(2)当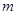 在什么范围内取值时,能使数列
在什么范围内取值时,能使数列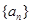 满足不等式
满足不等式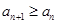 恒成立?
恒成立?
(3)当 时,证明:
时,证明: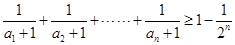 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com