
(本小题共2小题,每小题6分,满分12分)
(1)已知梯形ABCD是直角梯形,按照斜二测画法画出它的直观图 如图所示,其中
如图所示,其中 ,
, ,
, ,求直角梯形以BC为旋转轴旋转一周形成的几何体的表面积。
,求直角梯形以BC为旋转轴旋转一周形成的几何体的表面积。
(2)定线段AB所在的直线与定平面α相交,P为直线AB外的一点,且P不在α内,若直线AP、BP与α分别交于C、D点,求证:不论P在什么位置,直线CD必过一定点.

(1)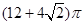 ;(2)不论P在什么位置,直线CD必过一定点.
;(2)不论P在什么位置,直线CD必过一定点.
【解析】本试题主要是考查了斜二测画法的运用,以及空间几何体中表面积的求解。
(1)由斜二测画法可知AB=2,BC=4,AD=2进而DC=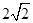 ,那么旋转得到的几何体的表面积可以解得。
,那么旋转得到的几何体的表面积可以解得。
(2)设定线段AB所在直线为l,与平面α交于O点,即l∩α=O.。∴AP、BP可确定一平面β且C∈β,D∈β.因为CD=α∩β.∴A∈β,B∈β.∴l⊂β.∴O∈β.∴O∈α∩β,即O∈CD.
解:(1)由斜二测画法可知AB=2,BC=4,AD=2
进而DC=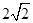 ,
,
旋转后形成的几何体的表面积

(2)设定线段AB所在直线为l,与平面α交于O点,即l∩α=O.
由题意可知,AP∩α=C,BP∩α=D,∴C∈α,D∈α.
又∵AP∩BP=P.
∴AP、BP可确定一平面β且C∈β,D∈β.
∴CD=α∩β.∴A∈β,B∈β.∴l⊂β.∴O∈β.∴O∈α∩β,即O∈CD.
∴不论P在什么位置,直线CD必过一定点.


科目:高中数学 来源: 题型:
|
|
| π |
| 3 |
| 2 |
查看答案和解析>>
科目:高中数学 来源:2014届浙江省杭州市高一第一学期阶段考试数学 题型:解答题
附加题:本大题共2小题,每小题10分,共20分。
(本题满分10分)已知函数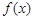 在
在 上为增函数,且f(
上为增函数,且f( )=
)= ,f(1)=2,集合
,f(1)=2,集合 ,关于
,关于 的不等式
的不等式 的解集为
的解集为 ,求使
,求使 的实数
的实数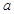 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2010-2011年浙江省杭州市高二下学期期中考试文数 题型:解答题
四、附加题:本大题共2小题,每小题10分,共20分。
(20)(本小题满分10分)
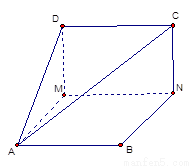
已知 是边长为1的正方形,
是边长为1的正方形,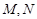 分别为
分别为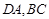 上的点,且
上的点,且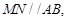 沿
沿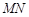 将正方形折成直二面角
将正方形折成直二面角 .
.
(I)求证:平面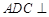 平面
平面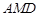 ;
;
(II)设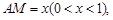 点
点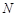 与平面
与平面 间的距离为
间的距离为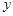 ,试用
,试用 表示
表示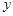 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数
(1)在给定的直角坐标系内画出![]() 的图象;
的图象;
(2)写出![]() 的单调递增区间(不需要证明);
的单调递增区间(不需要证明);
(3)写出![]() 的最大值和最小值(不需要证明).
的最大值和最小值(不需要证明).
(第II卷) 50分
一、填空题(本大题共2小题,每小题4分,共8分.把答案填在答题卡上)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com