
| 1 |
| 10 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
| x |
| 10 |
| 2 |
| 5 |
| 1 |
| 10 |
| 2 |
| 55-5x |
| 7 |
| 10 |
| 2 |
| 5 |
| 10-b |
| 10 |


 天天练口算系列答案
天天练口算系列答案科目:高中数学 来源: 题型:
| 1 |
| 10 |
| 2 |
| 5 |
查看答案和解析>>
科目:高中数学 来源:山东模拟 题型:解答题
| 1 |
| 10 |
| 2 |
| 5 |
查看答案和解析>>
科目:高中数学 来源:2010-2011学年河南省高三上学期九月月考理科数学卷 题型:解答题
(本小题满分12分)
某电视生产厂家有A、B两种型号的电视机参加家电下乡活动.若厂家投放A、B型号电视机的价值分别为p、q万元,农民购买电视机获得相应的补贴分别为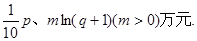 已知厂家把价值为10万元的A、B两种型号的电视机投放市场,且A、B两种型号的电视机投放金额都不低于1万元(精确到0.1,参考数据:
已知厂家把价值为10万元的A、B两种型号的电视机投放市场,且A、B两种型号的电视机投放金额都不低于1万元(精确到0.1,参考数据: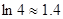 ).
).
(1)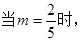 请你制定一个投放方案,使得在这次活动中农民得到的补贴最多,并求出其最大值;
请你制定一个投放方案,使得在这次活动中农民得到的补贴最多,并求出其最大值;
(2)讨论农民得到的补贴随厂家投放B型号电视机金额的变化而变化的情况.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年江西省赣州市会昌中学高三(上)第二次月考数学试卷(理科)(解析版) 题型:解答题
 万元.已知厂家把总价值为10万元的A、B两种型号电视机投放电场,且A、B型号的电视机投放金额不低于1万元,请你制订一个投放方案,使得在这次活动中农民得到的补贴最多,并求出最大值(精确到0.1,参考数据:ln4=1.4)
万元.已知厂家把总价值为10万元的A、B两种型号电视机投放电场,且A、B型号的电视机投放金额不低于1万元,请你制订一个投放方案,使得在这次活动中农民得到的补贴最多,并求出最大值(精确到0.1,参考数据:ln4=1.4)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com