Question

如图，某水产养殖场拟造一平面图为矩形且面积为160平方米的水产养殖网箱，为了避免混养，箱中要安装一些筛网，如果网箱四周网衣（图中实线部分）建造单价为每米长112元，筛网（图中虚线部分）的建造单价为每米长96元，网箱底面建造单价为每平方米100元，网衣及筛网厚度均忽略不计，要求网箱的长与宽都不能超过15米.

___________________.（先在横线上填上一个结论，然后再解答）

Answer 1

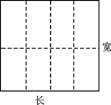
构建问题：如图，某水产养殖场拟造一平面图为矩形且面积为160平方米的水产养殖网箱，为了避免混养，箱中要安装一些筛网，如果网箱四周网衣（图中实线部分）建造单价为每米长112元，筛网（图中虚线部分）的建造单价为每米长96元，网箱底面建造单价为每平方米100元，网衣及筛网厚度均忽略不计，要求网箱的长与宽都不能超过15米.则当网箱的长与宽各为多少米时，可使总造价最低？（精确到0.01米）

解析：设网箱的总造价为y（元），网箱的长为x，则

y=112(2x+×2)+96(x+×3)+100×160

=320(x+)+16 000（≤x≤15）.

由于函数在［，15］上是减函数，

∴当x=15米时，y有最小值，

此时，网箱的宽为≈10.67米.

∴当网箱长15米，宽10.67米时，总造价最低.