练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    椭圆C1：数学公式=1（a＞b＞0）的左右顶点分别为A、B．点P双曲线C2：数学公式=1在第一象限内的图象上一点，直线AP、BP与椭圆C1分别交于C、D点．若△ACD与△PCD的面积相等．
    （1）求P点的坐标；
    （2）能否使直线CD过椭圆C1的右焦点，若能，求出此时双曲线C2的离心率，若不能，请说明理由．

    解：（1）设P（x0，y0）（x0＞0，y0＞0），又有点A（-a，0），B（a，0）．
    ∵S△ACD=S△PCD，
    ∴C为AP的中点，∴．
    将C点坐标代入椭圆方程，得，
    又，
    ∴x0=2a（x0=-a舍去），
    ∴，
    ∴．
    （2）∵，
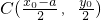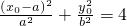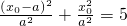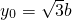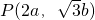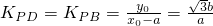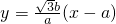    直线PD：代入?2x2-3ax+a2=0
    ∴，
    ∴
    ∴CD垂直于x轴．若CD过椭圆C1的右焦点，则，
    ∴，
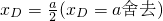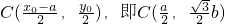
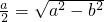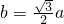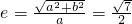    ∴．故可使CD过椭圆C1的右焦点，此时C2的离心率为．
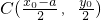    分析：（1）设P（x0，y0）（x0＞0，y0＞0），又有点A（-a，0），B（a，0）．由S△ACD=S△PCD，知C为AP的中点，．将C点坐标代入椭圆方程，得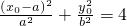，由此能够推导出．
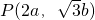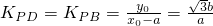    （2）由，把直线PD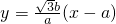：代入?2x2-3ax+a2=0．由此入手能够导出可使CD过椭圆C1的右焦点，此时C2的离心率为．
    点评：本题考查直线和圆锥曲线的位置关系，解题时要认真审题，注意合理地进行等价转化．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    （08年宁夏、海南卷理）（本小题满分12分）在直角坐标系xOy中，椭圆C1：=1（a＞b＞0）的左、右焦点分别为F1，F2．F2也是抛物线C2：的焦点，点M为C1与C2在第一象限的交点，且｜MF2｜=．

    （Ⅰ）求C1的方程；

    （Ⅱ）平面上的点N满足，直线l∥MN，且与C1交于A，B两点，若，求直线l的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在直角坐标系xOy中，椭圆C1：=1（a＞b＞0）的左、右焦点分别为F1，F2．F2也是抛物线C2：的焦点，点M为C1与C2在第一象限的交点，且｜MF2｜=．

    （Ⅰ）求C1的方程；

    （Ⅱ）平面上的点N满足，直线l∥MN，且与C1交于A，B两点，若，求直线l的方程．

    查看答案和解析>>

    科目：高中数学 来源：2014届山东省济宁市高二上学期期末文科数学试卷（解析版） 题型：解答题

    在直角坐标系xOy中,椭圆C1: ="1" (a＞b＞0)的左、右焦点分别为F1、F2, F2也是抛物线C2：y2=4x的焦点，点M为C1与C2在第一象限的交点，且|MF2|=.

    （1）求C1的方程；

    （2）直线l∥OM，与C1交于A、B两点，若·=0，求直线l的方程.

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知椭圆C1：数学公式+数学公式=1（a＞b＞0）的离心率为数学公式，直线l：x-y+数学公式=0与椭圆C1相切．
    （1）求椭圆C1的方程；
    （2）设椭圆C1的左焦点为F1，右焦点为F2，直线l1过点F1且垂直与椭圆的长轴，动直线l2垂直于直线l1于点P，线段PF2的垂直平分线交l2于点M，求点M的轨迹C2的方程；
    （3）若A（x1，2），B（x2，y2），C（x0，y0）是C2上不同的点，且AB⊥BC，求实数y0的取值范围．

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年陕西省西安市远东一中高二（上）12月月考数学试卷（理科）（解析版） 题型：选择题

    以椭圆C1：+=1（a、b＞0）焦点为顶点，以椭圆C1的顶点为焦点的双曲线C2，下列结论中错误的是（ ）
    A．C2的方程为 =1
    B．C1、C2的离心率的和是1
    C．C1、C2的离心率的积是1
    D．短轴长等于虚轴长

    查看答案和解析>>

    同步练习册答案