
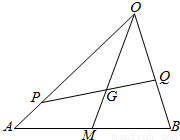
 如图,G是△OAB的重心,P、Q分别是边OA、OB上的动点,且P、G、Q三点共线.
如图,G是△OAB的重心,P、Q分别是边OA、OB上的动点,且P、G、Q三点共线.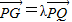 ,将
,将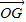 用λ、
用λ、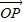 、
、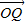 表示;
表示;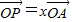 ,
,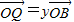 ,证明:
,证明: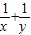 是定值;
是定值;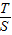 的取值范围.
的取值范围. 的图形△OPG,利用向量的加法法则知
的图形△OPG,利用向量的加法法则知 ,在根据
,在根据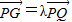 和
和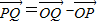 即可
即可 ,
, 知:
知: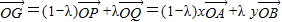 在根据G是△OAB的重心知:
在根据G是△OAB的重心知: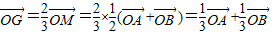 ,最后根据
,最后根据 、
、 不共线得到关于x,y,λ的方程组即可求解
不共线得到关于x,y,λ的方程组即可求解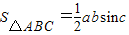 ,知
,知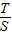 =xy,由点P、Q的定义知
=xy,由点P、Q的定义知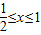 ,
,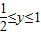 ,
,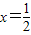 时,y=1;x=1时,
时,y=1;x=1时, .此时,均有
.此时,均有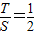 .
.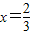 时,
时,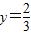 .此时,均有
.此时,均有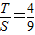 .得到
.得到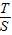 的范围为
的范围为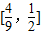 在根据(2)知
在根据(2)知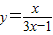 进行作差证明即可
进行作差证明即可 =
=
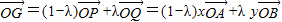 ;①
;①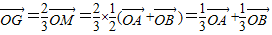 .②
.②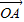 、
、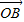 不共线,∴由①、②,
不共线,∴由①、②,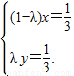
 ,
,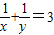 (定值).
(定值).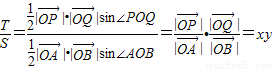 .
. ,
,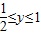 ,
, 时,y=1;x=1时,
时,y=1;x=1时,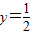 .
. .
.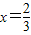 时,
时,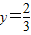 .
.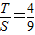 .
.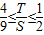 .
.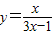 ,
,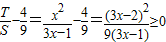 ,
,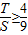 .
.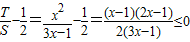 ,
,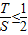 .
.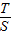 的取值范围
的取值范围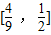 .
.

 名师点拨卷系列答案
名师点拨卷系列答案科目:高中数学 来源: 题型:
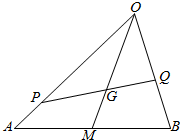 如图,G是△OAB的重心,P、Q分别是边OA、OB上的动点,且P、G、Q三点共线.
如图,G是△OAB的重心,P、Q分别是边OA、OB上的动点,且P、G、Q三点共线.| PG |
| PQ |
| OG |
| OP |
| OQ |
| OP |
| OA |
| OQ |
| OB |
| 1 |
| x |
| 1 |
| y |
| T |
| S |
查看答案和解析>>
科目:高中数学 来源: 题型:
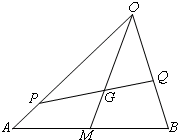 如图,G是△OAB的重心,P、Q分别是边OA、OB上的动点,且P、G、Q三点共线.
如图,G是△OAB的重心,P、Q分别是边OA、OB上的动点,且P、G、Q三点共线.| PG |
| PQ |
| OG |
| OP |
| OQ |
| OP |
| OA |
| OQ |
| OB |
| 1 |
| x |
| 1 |
| y |
查看答案和解析>>
科目:高中数学 来源:2011-2012学年山东省济宁市梁山一中高一(下)期中数学试卷(解析版) 题型:解答题
 如图,G是△OAB的重心,P、Q分别是边OA、OB上的动点,且P、G、Q三点共线.
如图,G是△OAB的重心,P、Q分别是边OA、OB上的动点,且P、G、Q三点共线.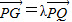 ,将
,将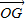 用λ、
用λ、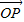 、
、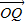 表示;
表示;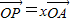 ,
,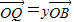 ,证明:
,证明: 是定值;
是定值;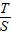 的取值范围.
的取值范围.查看答案和解析>>
科目:高中数学 来源:2012-2013学年陕西省榆林市神木中学高三(上)数学寒假作业3(理科)(解析版) 题型:解答题
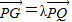 ,将
,将 用λ、
用λ、 、
、 表示;
表示;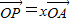 ,
,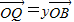 ,证明:
,证明: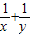 是定值.
是定值.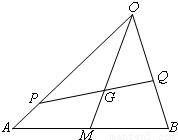
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com