【答案】
分析:(1)将圆O
1的方程化为标准方程,找出O
1的坐标,由P,Q两点关于直线l对称,得到直线l过O
1,又直线l过A点,由两点的坐标写出直线l的方程即可;
(2)设O
2的坐标为(a,b),由O
2与点A关于直线x+3y=0对称,得到O
2与点A的中点在x+3y=0上,利用线段中点坐标公式表示出O
2与点A的中点坐标,代入x+3y=0中,得到关于a与b的方程,且直线O
2A与直线x+3y=0垂直,得到斜率的乘积为-1,由直线x+3y=0的斜率求出直线O
2A的斜率,由O
2与点A的坐标表示出斜率,列出关于a与b的方程,联立两方程求出a与b的值,确定出O
2的坐标,设圆O
2的半径为r,表示出圆O
2的方程,两圆的方程相减得到公共弦MN所在直线的方程,利用点到直线的距离公式表示出圆心O
2到直线MN的距离,即为弦心距,根据勾股定理由弦MN长的一半,圆的半径r及弦心距列出关于r的方程,求出方程的解得到r的值,即可确定出圆O
2的方程.
解答:解:(1)将圆O
1的方程化为标准方程得:x
2+(y+1)
2=4,
∴O
1(0,-1),又P,Q两点关于过定点A的直线l对称,
∴O
1(0,-1)在直线l上,又直线l过A(1,-2),
∴直线l的方程为y+2=
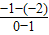
(x-1),即x+y+1=0;
(2)设O
2(a,b),
∵O
2与A关于直线x+3y=0对称,且x+3y=0的斜率为-

,
∴
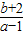
=3①,且
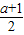
+3•

=0②,
联立①②解得:a=2,b=1,∴O
2(2,1),
可设圆O
2的方程为:(x-2)
2+(y+1)
2=r
2,
又圆O
1的方程为:x
2+(y+1)
2=4,
∴两圆方程相减,即得两圆公共弦MN所在直线的方程为4x+4y+r
2-8=0,
∵|MN|=2
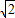
,圆O
1的半径为2,
∴O
1到直线MN的距离为
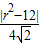
=

=
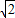
,
解得:r
2=20或r
2=4,
则圆O
2的方程为:(x-2)
2+(y+1)
2=20或(x-2)
2+(y+1)
2=4.
点评:此题考查了直线与圆的位置关系,涉及的知识有:关于点、直线对称的直线方程,直线的两点式方程,线段中点坐标公式,两圆相交的性质,点到直线的距离公式,垂径定理,勾股定理,以及圆的标准方程,当直线与圆相交时,常常根据垂径定理由垂直得中点,然后由弦长的一半,圆的半径及弦心距构造直角三角形,利用勾股定理来解决问题.

 内一定点A(1,-2),P,Q为圆上的两不同动点.
内一定点A(1,-2),P,Q为圆上的两不同动点. ,求圆O2的方程.
,求圆O2的方程.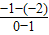 (x-1),即x+y+1=0;
(x-1),即x+y+1=0; ,
,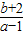 =3①,且
=3①,且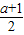 +3•
+3• =0②,
=0②,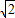 ,圆O1的半径为2,
,圆O1的半径为2,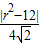 =
= =
=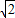 ,
,

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案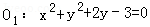 内一定点A(1,﹣2),P,Q为圆上的两不同动点.
内一定点A(1,﹣2),P,Q为圆上的两不同动点.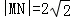 ,求圆O2的方程.
,求圆O2的方程. 内一定点A(1,-2),P,Q为圆上的两不同动点.
内一定点A(1,-2),P,Q为圆上的两不同动点. ,求圆O2的方程.
,求圆O2的方程.