
 .如果二面角α-AB-β=60°,那么A、B两点的球面距离为( )
.如果二面角α-AB-β=60°,那么A、B两点的球面距离为( ) π
π π
π

 ,二面角α-AB-β=60°,我们易求出球的半径,易弦AB的球心角,代入弧长公式,即可求出答案.
,二面角α-AB-β=60°,我们易求出球的半径,易弦AB的球心角,代入弧长公式,即可求出答案. .
.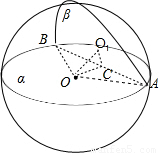
 ,OC=4.
,OC=4.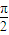 .
.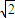 ,所以A、B两点间的球面距离为4
,所以A、B两点间的球面距离为4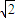 ×
×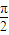 =2
=2 π
π

 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案科目:高中数学 来源: 题型:
| 3 |
A、2
| ||
B、
| ||
C、
| ||
D、
|
查看答案和解析>>
科目:高中数学 来源:2010年河北省唐山一中高考数学冲刺试卷1(文科)(解析版) 题型:选择题
 .如果二面角α-AB-β=60°,那么A、B两点的球面距离为( )
.如果二面角α-AB-β=60°,那么A、B两点的球面距离为( ) π
π π
π

查看答案和解析>>
科目:高中数学 来源: 题型:
已知A、B是球O表面上两点,AB=8.过AB作两个平面α、β,使球心O在平面α上,且O到平面β的距离为2![]() .如果二面角α—AB—β=60°,那么A、B两点的
.如果二面角α—AB—β=60°,那么A、B两点的
球面距离为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
已知A、B是球O表面上两点,AB=8.过AB作两个平面α、β,使球心O在平面
α上,且O到平面β的距离为2![]() .如果二面角α—AB—β=60°,那么A、B两点间的球面距离为 ( )
.如果二面角α—AB—β=60°,那么A、B两点间的球面距离为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com