若实数x,y满足x2+y2+2x-2y+1=0,则2y-2x-1的最小值为________.
分析:把x与y满足的等式配方后,得到圆的标准方程,设出圆的参数方程,得到x=cosα-1,y=sinα+1,代入所求的式子中,利用特殊角的三角函数值及两角和的正弦函数公式化为一个角的正弦函数,由正弦函数的值域即可得到2y-2x-1的最小值.
解答:由题意,圆的标准方程为(x+1)
2+(y-1)
2=1,
设圆的参数方程,x=cosα-1,y=sinα+1
∴

)+3
由sin(

)∈[-1,1],
∴2y-2x-1的最小值为
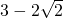
故答案为
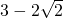
点评:本题的考点是直线和圆的方程的应用,主要考查学生掌握圆的参数方程,灵活运用两角和的正弦函数公式化简求值,是一道基础题.本题的突破点是将已知的等式配方后得到一个圆的方程.

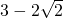
 )+3
)+3 )∈[-1,1],
)∈[-1,1],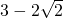


 53随堂测系列答案
53随堂测系列答案