
 ,由于
,由于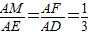 ,可得MF∥ED,则∠CFM或其补角,即为异面直线DE与CF的夹角.利用余弦定理求得CF2、MF2、CM2 的值,再在△CFM中,利用余弦定理求得cos∠CFM 得值,再取绝对值,即得所求.
,可得MF∥ED,则∠CFM或其补角,即为异面直线DE与CF的夹角.利用余弦定理求得CF2、MF2、CM2 的值,再在△CFM中,利用余弦定理求得cos∠CFM 得值,再取绝对值,即得所求. 解:∵在棱长为3的正四面体ABCD中,点E是线段AB上一点,且AE=1,点F是线段AD上一点,且AF=2,
解:∵在棱长为3的正四面体ABCD中,点E是线段AB上一点,且AE=1,点F是线段AD上一点,且AF=2, ,如图所示:
,如图所示: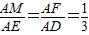 ,∴MF∥ED,则∠CFM或其补角,即为异面直线DE与CF的夹角.
,∴MF∥ED,则∠CFM或其补角,即为异面直线DE与CF的夹角. -2×3×
-2×3× ×cos60°=
×cos60°= ,
, +1-2×
+1-2× ×1×cos60°=
×1×cos60°= .
.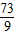 =7+
=7+ -2×
-2×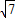 ×
×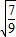 ×cos∠CFM,解得cos∠CFM=-
×cos∠CFM,解得cos∠CFM=-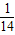 ,
,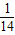 ,
,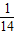 .
.

科目:高中数学 来源: 题型:
| A1A2 |
| AiAj |
| A、6 | B、5 | C、3 | D、2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 14 |
| 1 |
| 14 |
查看答案和解析>>
科目:高中数学 来源:2010年江西省新余一中 宜春中学 高安中学高二上学期第三次阶段考试理科数学卷 题型:填空题
在棱长为3的正四面体ABCD中,点E是线段AB上一点,且AE="1," 点F是线段AD上一点,且AF=2,则异面直线DE与CF的夹角的余弦为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com