
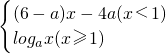 是(-∞,+∞)上的增函数,则实数a的取值范围是
是(-∞,+∞)上的增函数,则实数a的取值范围是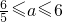 }
}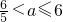 }
}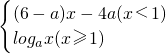 是(-∞,+∞)上的增函数,故当x<1时,f(x)=(6-a)x-4a<0;综合可解得实数a的取值范围.
是(-∞,+∞)上的增函数,故当x<1时,f(x)=(6-a)x-4a<0;综合可解得实数a的取值范围.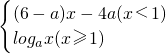 是(-∞,+∞)上的增函数,
是(-∞,+∞)上的增函数,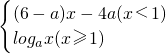 是(-∞,+∞)上的增函数,x≥1时,f(x)=logax≥0;
是(-∞,+∞)上的增函数,x≥1时,f(x)=logax≥0; ④
④ ≤a<6.
≤a<6.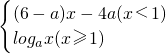 是(-∞,+∞)上的增函数”的分段讨论与整体把握,特别是对“当x<1时,f(x)=(6-a)x-4a<0”的理解与应用,易错点在于忽略“f(1)=(6-a)•1-4a≤0”中的等号,属于难题.
是(-∞,+∞)上的增函数”的分段讨论与整体把握,特别是对“当x<1时,f(x)=(6-a)x-4a<0”的理解与应用,易错点在于忽略“f(1)=(6-a)•1-4a≤0”中的等号,属于难题. 

科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com