
(I) 证明![]() 平面
平面![]() ;
;
(II)若![]() 为正三角形,试判断点
为正三角形,试判断点![]() 在平面
在平面![]() 内的射影
内的射影![]() 是否在直线
是否在直线![]() 上,证明你的结论,并求角
上,证明你的结论,并求角![]() 的余弦值.
的余弦值.

本小题主要考查空间中的线面关系,解三角形等基础知识,考查空间想象能力和思维能力.

(Ⅰ)证明:E、F分别是正方形ABCD的边AB、CD的中点.
∴EB∥FD.且EB=FD.
∴四边形EBFD是平行四边形.
∴BF∥ED.
∵ED![]() 平面AED.而BF
平面AED.而BF![]() 平面AED.
平面AED.
∴BF∥平面AED
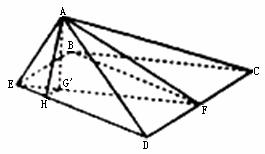
(Ⅱ)解法一:点A在平面BCDE内的射影G在直线EF上.
过点A作AG⊥平面BCDE.垂足为G,连结GC、GD.
∵△ACD为正三角形.
∴AC=AD.
∴GC=GD.
∴G在CD的垂直平分线上.
又∵EF是CD的垂直平分线.
∴点A在平面BCDE内的射影G在直线EF上.
过G作GH⊥ED.垂足为H,连结AH,则AH⊥DE.
∴∠AHG是二面角A-DE-C的平面角,即∠AHG=θ.
设原正方形ABCD的边长为
在折后图的△AEF中,AF=![]() a,EF=2AE=
a,EF=2AE=
∴△AEF为直角三角形,AG·EF=AE·AF.
∴AG=![]()
在Rt△ADE中,AH·DE=AD·AE.
∴AH=![]()
∴GH=![]()
∴cosθ=![]()
解法二:点A在平面BCDE内的射影G在直线EF上.
连结AF,在平面AEF内过点A作AG′⊥EF.垂足为G′.
∵△ACD为正三角形,F为CD的中点.
∴AF⊥CD.
又∵EF⊥CD.
∴CD⊥平面AEF.
∵AG′![]() 平面AEF.
平面AEF.
∴CD⊥AG′.
又∵AG′⊥EF,且CD∩EF=F,CD![]() 平面BCDE,EF
平面BCDE,EF![]() 平面BCDE.
平面BCDE.
∴AG′⊥平面BCDE.
∴G′为A在平面BCDE内的射影G.
∴点A在平面BCDE内的射影G在直线EF上.
过G作GH⊥ED,垂足为H,连结AH,则AH⊥DE.
∴∠AHG是二面角A-DE-C的平面角,即∠AHG=θ.
设原正方形ABCD的边长为
在折后图的△AEF中,AF=![]() EF=2AE=
EF=2AE=
∴△AEF为直角三角形,AG·EF=AE·AF,
∴AG=![]()
在Rt△ADE中,AH·DE=AD·AE,
∴AH=![]()
∴GH=![]()
∴cosθ=![]()
解法三:点A在平面BCDE内的射影G在直线EF上.
连结AF,在平面AEF内过点A作AG′⊥EF,垂足为G′,
∵△ACD为正三角形,F为CD中点,
∴AF⊥CD.
又∵EF⊥CD,
∴CD⊥平面AEF.
∵CD![]() 平面BCDE.
平面BCDE.
∴平面AEF⊥平面BCDE.
又∵平面AEF∩平面BCDE=EF,AG′⊥EF,
∴AG′⊥平面BCDE,即G′为A在平面BCDE内的射影G,
∴点A在平面BCDE内的射影G在直线EF上.
过G作GH⊥DE,垂足为H,连结AH,则AH⊥DE.
∴∠AHG是二面角A-DE-C的平面角,即∠AHG=θ.
设原正方形ABCD的边长为
在折后图的△AEF中,AF=![]() EF=2AE=
EF=2AE=
∴△AEF为直角三角形,AG·EF=AE·AF.
∴AG=![]()
在Rt△ADE中,AH·DE=AD·AE.
∴AH=![]()
∴GH=![]()
∴cosθ=![]()


科目:高中数学 来源: 题型:
A、
| ||
B、
| ||
C、
| ||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 |
| 6 |
| A、9π | B、12π |
| C、18π | D、6π |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年河南省原名校高三下学期第二次联考文科数学试卷(解析版) 题型:选择题
已知长方体ABCD—A1B1ClD1内接于球O,底面ABCD是边长为2的正方形,E为AA1的中点,OA⊥平面BDE,则球O的表面积为
A.8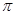 B.16
B.16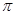 : C.14
: C.14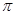 D.18
D.18
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com