
在数列 中,
中, 为常数,
为常数, ,
, 构成公比不等
构成公比不等
于 的等比数列.记
的等比数列.记  (
( .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)设 的前
的前 项和为
项和为 ,是否存在正整数
,是否存在正整数 ,使得
,使得 成立?若存在,找出一个正整数
成立?若存在,找出一个正整数 ;若不存在,请说明理由.
;若不存在,请说明理由.
(1)2;(2)见解析
解析试题分析:(1)等差数列基本量的求解是等差数列的一类基本问题,解决这类问题的关键在于熟练掌握等差数列的有关公式并能灵活运用;解决等比数列这类问题尤其需要注意的是,在使用等比数列的前 项和公式时,应该要分类讨论,有时还应善于运用整体代换的思想简化运算过程;(3)观测数列的特点形式,看使用什么方法求和.使用裂项法求和时,要注意正负项相消时消去了哪些项,保留了哪些项,切不可漏写未被消去的项,未被消去的项有前后对称的特点,实质上造成正负相消是此法的根源和目的.(4)在做题时注意观察式子特点选择有关公式和性质进行化简,这样给做题带来方便,掌握常见求和方法,如分组转化求和,裂项法,错位相减.
项和公式时,应该要分类讨论,有时还应善于运用整体代换的思想简化运算过程;(3)观测数列的特点形式,看使用什么方法求和.使用裂项法求和时,要注意正负项相消时消去了哪些项,保留了哪些项,切不可漏写未被消去的项,未被消去的项有前后对称的特点,实质上造成正负相消是此法的根源和目的.(4)在做题时注意观察式子特点选择有关公式和性质进行化简,这样给做题带来方便,掌握常见求和方法,如分组转化求和,裂项法,错位相减.
试题解析:(Ⅰ)∵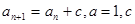 为常数,∴
为常数,∴ 是以
是以 为首项,
为首项, 为公差的等差数列,∴
为公差的等差数列,∴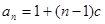 .
.
∴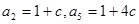 .又
.又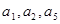 成等比数列,∴
成等比数列,∴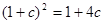 ,
,
解得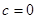 或
或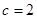 .
.
当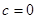 时,
时,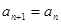 不合题意,舍去.∴
不合题意,舍去.∴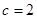 .
.
(Ⅱ)由(Ⅰ)知,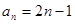 .
.
∴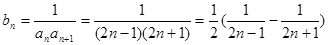
∴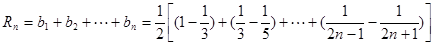
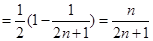 .
.
假设存在正整数 ,使得
,使得 ,即
,即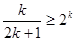
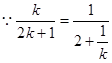 随
随 的增大而增大,
的增大而增大,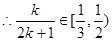 ,而
,而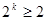
所以不存在正整数 ,使得
,使得 成立.
成立.
考点:等比数列的定义及性质的应用.


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com