解:(1)由 α=2kπ
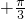
(k∈Z),可推出 tanα=

,但 tanα=

时,α=kπ
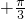
,不能推出 α=2kπ
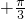
,
故α=2kπ
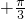
(k∈Z)是tanα=

的充分不必要条件,故(1)正确.
(2)函数y=sinxcosx=

sin2x,它的最小正周期是 π,故②不正确.
(3)在△ABC中,若cosAcosB>sinAsinB,则cos(A+B)>0,故A+B 为锐角,故C为钝角,故△ABC为钝角三角形,
故(3)正确.
(4)令sin(2x+

)=0,可得2x+

=kπ,x=
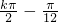
,k∈z,故函数y=2sin(2x+

)图象的对称中心为
(
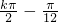
,0),故函数y=2sin(2x+

)+1图象的对称中心为(
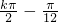
,1),故(4)正确.
(5)女大学生的身高预报体重的回归方程y′=0.849x-85.712,对于身高为172cm的女大学生可以得到其体重大约为
60.316(kg),故(5)不正确.
故答案为 (1)、(3)、(4).
分析:(1)由 α=2kπ
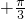
(k∈Z),可推出 tanα=

,但 tanα=

时,α=kπ
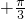
,不能推出 α=2kπ
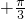
,故(1)正确.
(2)函数y=sinxcosx=

sin2x,它的最小正周期是 π,故②不正确.
(3)在△ABC中,若cosAcosB>sinAsinB,则cos(A+B)>0,故C为钝角,故△ABC为钝角三角形,故(3)正确.
(4)令sin(2x+

)=0,x=
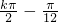
,k∈z,故函数y=2sin(2x+

)图象的对称中心为(
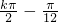
,0),
故函数y=2sin(2x+

)+1图象的对称中心为 (
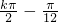
,1),故(4)正确.
(5)把x=172 代入回归方程y′=0.849x-85.712,得到y′=60.316,故女大学生的体重大约为60.316(kg),故(5)不正确.
点评:本题考查正弦函数的周期性,根据三角函数的值求角,正弦函数的对称性,回归直线方程,掌握三角函数的性质和
回归直线方程的意义,是解题的关键.

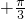 (k∈Z)是tanα=
(k∈Z)是tanα= 的充分不必要条件
的充分不必要条件 )+1图象的对称中心为(
)+1图象的对称中心为( -
- ,1)(k∈R)
,1)(k∈R)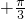 (k∈Z),可推出 tanα=
(k∈Z),可推出 tanα= ,但 tanα=
,但 tanα= 时,α=kπ
时,α=kπ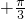 ,不能推出 α=2kπ
,不能推出 α=2kπ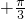 ,
,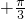 (k∈Z)是tanα=
(k∈Z)是tanα= 的充分不必要条件,故(1)正确.
的充分不必要条件,故(1)正确. sin2x,它的最小正周期是 π,故②不正确.
sin2x,它的最小正周期是 π,故②不正确. )=0,可得2x+
)=0,可得2x+ =kπ,x=
=kπ,x=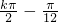 ,k∈z,故函数y=2sin(2x+
,k∈z,故函数y=2sin(2x+ )图象的对称中心为
)图象的对称中心为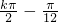 ,0),故函数y=2sin(2x+
,0),故函数y=2sin(2x+ )+1图象的对称中心为(
)+1图象的对称中心为(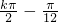 ,1),故(4)正确.
,1),故(4)正确.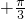 (k∈Z),可推出 tanα=
(k∈Z),可推出 tanα= ,但 tanα=
,但 tanα= 时,α=kπ
时,α=kπ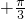 ,不能推出 α=2kπ
,不能推出 α=2kπ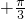 ,故(1)正确.
,故(1)正确. sin2x,它的最小正周期是 π,故②不正确.
sin2x,它的最小正周期是 π,故②不正确. )=0,x=
)=0,x=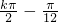 ,k∈z,故函数y=2sin(2x+
,k∈z,故函数y=2sin(2x+ )图象的对称中心为(
)图象的对称中心为(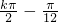 ,0),
,0), )+1图象的对称中心为 (
)+1图象的对称中心为 (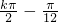 ,1),故(4)正确.
,1),故(4)正确.

 阅读快车系列答案
阅读快车系列答案 +sin1;(3)函数y=arccosx-
+sin1;(3)函数y=arccosx- 是偶函数.其中所有错误的命题序号是 .
是偶函数.其中所有错误的命题序号是 .