
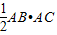 ,BD=4,DC=3,求AD的长;
,BD=4,DC=3,求AD的长;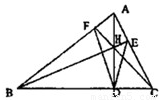
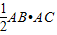 ,则A=90°,由射影定理求得斜边上的高AD的值.
,则A=90°,由射影定理求得斜边上的高AD的值.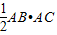 ,则A=90°,由射影定理可得 AD2=BD•CD=4×3=12,∴AD=2
,则A=90°,由射影定理可得 AD2=BD•CD=4×3=12,∴AD=2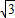 .
.


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案科目:高中数学 来源: 题型:
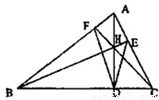
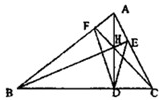 如图,AD是△ABC边BC上的高.
如图,AD是△ABC边BC上的高.| 1 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
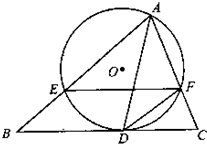
 (2012•江门一模)(几何证明选讲选做题)如图,AD是△ABC的高,AE是△ABC外接圆的直径.若AB=6,AC=5,AD=4,则图中与∠BAE相等的角是
(2012•江门一模)(几何证明选讲选做题)如图,AD是△ABC的高,AE是△ABC外接圆的直径.若AB=6,AC=5,AD=4,则图中与∠BAE相等的角是| 15 |
| 2 |
| 15 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2009•大连一模)选修4-1:几何证明选讲
(2009•大连一模)选修4-1:几何证明选讲查看答案和解析>>
科目:高中数学 来源:2012-2013学年河南省洛阳市高三(上)期中数学试卷(文科)(解析版) 题型:解答题
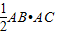 ,BD=4,DC=3,求AD的长;
,BD=4,DC=3,求AD的长;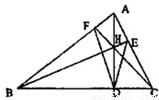
查看答案和解析>>
科目:高中数学 来源:2012-2013学年河南省洛阳市高三(上)期中数学试卷(文科)(解析版) 题型:解答题
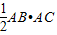 ,BD=4,DC=3,求AD的长;
,BD=4,DC=3,求AD的长;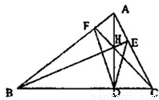
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com