练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    (08年泉州一中适应性练习理)（12分）已知函数.                                

    （1）求f (x)的单调区间；

    （2）若当时，不等式f (x)<m恒成立，求实数m的取值范围；

    （3）若关于x的方程在区间[0, 2]上恰好有两个相异的实根，求实数a的取值范围.

    解析：（1）函数的定义域为（-1, +∞）.…

           ∵ , 

    由，得x>0；由，得.

    ∴ f (x)的递增区间是，递减区间是（-1, 0）.

    （2）∵ 由，得x=0,x=-2（舍去）

    由（Ⅰ）知f (x)在上递减，在上递增. 

    又 ， , 且.

    ∴ 当时，f (x)的最大值为.

    故当时，不等式f (x)<m恒成立.

    （3）方程,  .

          记,

          ∵ ,  

    由,得x>1或x<-1（舍去）.   由, 得.

                 ∴ g(x)在[0,1]上递减, 在[1,2]上递增.

                 为使方程在区间[0, 2]上恰好有两个相异的实根，

                只须g(x)=0在[0,1]和上各有一个实数根,于是有

                ∵ , 

    ∴ 实数a的取值范围是 .

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：不详 题型：填空题

    已知A（5，2）、B（1，1）、C(1，
    22
    5
    )    ，在△ABC所在的平面区域内，若使目标函数z=ax+y（a＞0）取得最大值的最优解有无穷多个，则a的值为______．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    已知x，y满足不等式组
    x+y≤4
    ax+by-2a≤0
    ，且目标函数z=2x+y的最大值为7，则a+b=______．

    查看答案和解析>>

    科目：高中数学 来源：安徽省模拟题 题型：单选题

    P的坐标（x，y）满足，过点P的直线l与圆C：x2+y2=14相交于A、B两点，则|AB|的最小值是
    [     ]
    A．2
    B．4
    C．2
    D．3

    查看答案和解析>>

    科目：高中数学 来源：0107 模拟题 题型：填空题

    若实数x，y满足不等式组，则z=|x+2y-10|的最小值是（    ）。

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    已知变量x，y满足约束条件
    y≤2
    x+y≥1
    x-y≤1
    ，则z=3|x|+y的取值范围为（　　）
    A．[-1，5] B．[1，11] C．[5，11] D．[-7，11]

    查看答案和解析>>

    科目：高中数学 来源：醴陵市模拟 题型：单选题

    设集合A={（x，y）||x|+|y|≤1}，B={（x，y）|（y-x）（y+x）≤0}，M=A∩B，若动点P（x，y）∈M，则x2+（y-1）2的取值范围是（　　）
    A．[
    1
    2
    ，
    5
    2
    ]    		 B．[
    		2
    2
    ，
    5
    2
    ]    		 C．[
    1
    2
    ，
    		10
    2
    ]    		 D．[
    		2
    2
    ，
    		10
    2
    ]

    查看答案和解析>>

    科目：高中数学 来源：同步题 题型：填空题

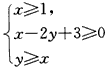    设不等式组所表示的平面区域Ω1，平面区域Ω2与Ω1关于直线3x-4y-9=0对称，对于Ω1中的任意一点A与Ω2中的任意一点B，|AB|的最小值等于（    ）。

    查看答案和解析>>

    科目：高中数学 来源：安徽省高考真题 题型：填空题

    若满足约束条件：；则的取值范围为（    ）。

    查看答案和解析>>

    同步练习册答案