
(2006年安徽卷)已知函数 在R上有定义,对任何实数
在R上有定义,对任何实数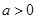 和任何实数
和任何实数 ,都有
,都有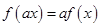
(Ⅰ)证明 ;
;
(Ⅱ)证明 其中
其中 和
和 均为常数;
均为常数;
(Ⅲ)当(Ⅱ)中的 时,设
时,设 ,讨论
,讨论 在
在 内的单调性并求极值.
内的单调性并求极值.
(Ⅰ)见解析。(Ⅱ)见解析。
(Ⅲ)当 时,函数
时,函数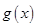 在
在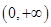 内取得极小值,极小值为
内取得极小值,极小值为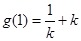
【解析】
试题分析:分析:(Ⅰ)抽象函数通过赋值法求解.
(Ⅱ)通过赋值,构做 的关系.
的关系.
(Ⅲ)利用(Ⅱ)中关系,表示出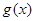 ,利用导数研究函数单调性与极值性.
,利用导数研究函数单调性与极值性.
证明(Ⅰ)令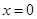 ,则
,则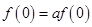 ,∵
,∵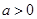 ,∴
,∴ 。
。
(Ⅱ)①令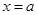 ,∵
,∵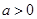 ,∴
,∴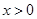 ,则
,则 。
。
假设 时,
时,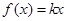
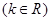 ,则
,则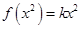 ,而
,而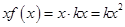 ,∴
,∴ ,即
,即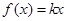 成立。
成立。
②令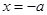 ,∵
,∵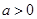 ,∴
,∴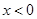 ,
,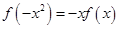
假设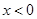 时,
时,
 ,则
,则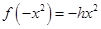 ,而
,而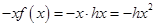 ,∴
,∴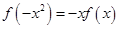 ,即
,即 成立。∴
成立。∴ 成立.
成立.
(Ⅲ)当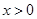 时,
时,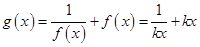 ,
,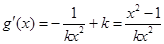
令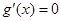 ,得
,得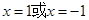 ;
;
当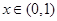 时,
时,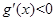 ,∴
,∴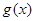 是单调递减函数;
是单调递减函数;
当 时,
时,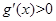 ,∴
,∴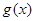 是单调递增函数;
是单调递增函数;
所以当 时,函数
时,函数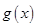 在
在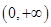 内取得极小值,极小值为
内取得极小值,极小值为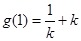
考点:本题主要考查分段函数、抽象函数及导数在研究单调性方面的应用。
点评:在抽象函数的求值和求解析式中要注意通过赋特殊值构造求解关系.


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com