解:由f(x+

)=-f(x),得f(x+3)=f[(x+

)+

]=-f(x+

)=f(x),则有周期T=3.
又∵f(x)的图象关于点
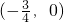
成中心对称,即f(

+x)=-f(

-x),
令x=

代入上式,得f(-

)=-f(-1),即f(1)=f(-

+

)=-f(-

)=f(-1)=1,
∵f(-1)=1,f(0)=-2,函数的周期是3,
∴f(1+3k)=f(-2)=1,f(2+3k)=f(-1)=1,f(3+3k)=f(0)=-2,其中k是任意整数.
则f(1)+f(2)+…+f(2009)=

[f(1)+f(2)+f(3)]+f(2008)+f(2009)
=669×(1+1-2)+f(1)+f(2)=2.
故答案为:2.
分析:根据题意需要反复给x恰当的值代入
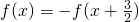
,求出函数的周期,再由函数图象关于点
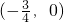
成中心对称,得到关系式f(

+x)=-f(

-x),利用条件和给x恰当的值求出函数在一个周期上的函数值,故求出一个周期内的函数值的和,根据函数的周期求式子的值.
点评:本题是一道抽象函数问题,题目的设计“小而巧”,解题的关键是巧妙的赋值,利用其奇偶性得到函数的周期性,再利用周期性求函数值.灵活的“赋值法”和反复利用恒等式是解决抽象函数问题的基本方法.

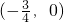 或中心对称,对任意的实数x均有
或中心对称,对任意的实数x均有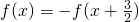 且f(-1)=1,f(0)=-2,则f(1)+f(2)+…+f(2009)的值为 ________.
且f(-1)=1,f(0)=-2,则f(1)+f(2)+…+f(2009)的值为 ________. )=-f(x),得f(x+3)=f[(x+
)=-f(x),得f(x+3)=f[(x+ )+
)+ ]=-f(x+
]=-f(x+ )=f(x),则有周期T=3.
)=f(x),则有周期T=3.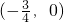 成中心对称,即f(
成中心对称,即f( +x)=-f(
+x)=-f( -x),
-x), 代入上式,得f(-
代入上式,得f(- )=-f(-1),即f(1)=f(-
)=-f(-1),即f(1)=f(- +
+ )=-f(-
)=-f(- )=f(-1)=1,
)=f(-1)=1, [f(1)+f(2)+f(3)]+f(2008)+f(2009)
[f(1)+f(2)+f(3)]+f(2008)+f(2009)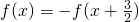 ,求出函数的周期,再由函数图象关于点
,求出函数的周期,再由函数图象关于点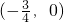 成中心对称,得到关系式f(
成中心对称,得到关系式f( +x)=-f(
+x)=-f( -x),利用条件和给x恰当的值求出函数在一个周期上的函数值,故求出一个周期内的函数值的和,根据函数的周期求式子的值.
-x),利用条件和给x恰当的值求出函数在一个周期上的函数值,故求出一个周期内的函数值的和,根据函数的周期求式子的值.
