
【题目】已知函数h(x)=ax3﹣1(a∈R),g(x)=lnx,f(x)=h(x)+3xg(x)(e为自然对数的底数).
(I)若f(x)图象过点(1,﹣1),求f(x)的单调区间;
(II)若f(x)在区间( ![]() ,e)上有且只有一个极值点,求实数a的取值范围;
,e)上有且只有一个极值点,求实数a的取值范围;
(III)函数F(x)=(a﹣ ![]() )x3+
)x3+ ![]() x2g(a)﹣h(x)﹣1,当a>e
x2g(a)﹣h(x)﹣1,当a>e ![]() 时,函数F(x)过点A(1,m)的切线至少有2条,求实数m的值.
时,函数F(x)过点A(1,m)的切线至少有2条,求实数m的值.
【答案】解:(Ⅰ)由已知f(x)=h(x)+3xg(x)=ax3﹣1+3xlnx,
又f(x)过点(1,﹣1),所以a=0,
∴f(x)=3xlnx﹣1,且定义域为(0,+∞),
f′(x)=3lnx+3=3(lnx+1),
令f′(x)>0,解得:x> ![]() ,令f′(x)<0,解得:0<x<
,令f′(x)<0,解得:0<x< ![]() ,
,
故f(x)=3xlnx﹣1在(0, ![]() )上是减函数,在(
)上是减函数,在( ![]() ,+∞)上是增函数;
,+∞)上是增函数;
(Ⅱ)函数f(x)=ax3+3xlnx﹣1的定义域为(0,+∞),
f′(x)=3(ax2+lnx+1),
令r(x)=ax2+lnx+1,
则r′(x)=2ax+ ![]() =
= ![]() ,
,
当a>0时,r′(x)>0在(0,+∞)恒成立,
故f′(x)=3(ax2+lnx+1)在(0,+∞)上是增函数,
而f′( ![]() )=
)= ![]() >0,
>0,
故当x∈( ![]() ,e)时,f′(x)>0恒成立,
,e)时,f′(x)>0恒成立,
故f(x)在区间( ![]() ,e)上单调递增,
,e)上单调递增,
故f(x)在区间( ![]() ,e)上没有极值点;
,e)上没有极值点;
当a=0时,由(Ⅰ)知,f(x)在区间( ![]() ,e)上没有极值点;
,e)上没有极值点;
当a<0时,令 ![]() =0,解得,x=
=0,解得,x= ![]() ;
;
故r(x)=ax2+lnx+1在(0, ![]() )上是增函数,在(
)上是增函数,在( ![]() ,+∞)上是减函数,
,+∞)上是减函数,
①当r(e)r( ![]() )<0,即﹣
)<0,即﹣ ![]() <a<0时,
<a<0时,
r(x)在( ![]() ,e)上有且只有一个零点,且在该零点两侧异号,
,e)上有且只有一个零点,且在该零点两侧异号,
②令r( ![]() )=0,得
)=0,得 ![]() =0,不成立;
=0,不成立;
③令r(e)=0,得a=﹣ ![]() ,所以
,所以 ![]() ∈(
∈( ![]() ,e),
,e),
而r( ![]() )=r(
)=r( ![]() )=
)= ![]() +ln
+ln ![]() >0,又r(
>0,又r( ![]() )<0,
)<0,
所以r(x)在( ![]() ,e)上有且只有一个零点,且在该零点两侧异号,
,e)上有且只有一个零点,且在该零点两侧异号,
综上所述,实数a的取值范围是[﹣ ![]() ,0).
,0).
(Ⅲ)函数F(x)=(a﹣ ![]() )x3+
)x3+ ![]() x2g(a)﹣h(x)﹣1,
x2g(a)﹣h(x)﹣1,
由函数F(x)过点A(1,m)的切线,
所以m= ![]() x03﹣(1+
x03﹣(1+ ![]() lna)x02+x0lna,(*)
lna)x02+x0lna,(*)
②据题意,原命题等价于关于x0的方程(*)至少有2个不同的解.
设φ(x)= ![]() x3﹣(1+
x3﹣(1+ ![]() lna)x2+xlna,
lna)x2+xlna,
φ′(x)=2x2﹣(2+lna)x+lna=(x﹣1)(2x﹣lna),
因为a> ![]() ,所以
,所以 ![]() lna>
lna> ![]() >1,
>1,
当x∈(﹣∞,1)和( ![]() lna,+∞)时,φ′(x)>0,φ(x)为增函数;
lna,+∞)时,φ′(x)>0,φ(x)为增函数;
当x∈(1, ![]() lna)时,φ′(x)<0,φ(x)为减函数;
lna)时,φ′(x)<0,φ(x)为减函数;
所以φ(x)的极大值为φ(1)= ![]() lna﹣
lna﹣ ![]() ,
,
φ(x)的极小值为φ( ![]() lna)=﹣
lna)=﹣ ![]() ln3a+
ln3a+ ![]() ln2a,
ln2a,
设lna=t,t> ![]() ,
,
则原命题等价于 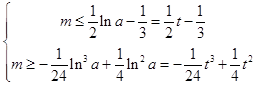 对t>
对t> ![]() 恒成立,
恒成立,
所以由m≤ ![]() t﹣
t﹣ ![]() 对t>
对t> ![]() 恒成立,得m≤
恒成立,得m≤ ![]() ; (1)
; (1)
记s(t)=﹣ ![]() t3+
t3+ ![]() t2 , s′(t)=﹣
t2 , s′(t)=﹣ ![]() t2+
t2+ ![]() t=
t= ![]() t(1﹣
t(1﹣ ![]() t),
t),
所以t> ![]() 时,s(t)的最大值为s(4)=
时,s(t)的最大值为s(4)= ![]() ,由m≥﹣
,由m≥﹣ ![]() t3+
t3+ ![]() t2对t>
t2对t> ![]() 恒成立,得m≥
恒成立,得m≥ ![]() . (2)
. (2)
由(1)(2)得,m= ![]() .
.
综上,当a> ![]() ,实数m的值为
,实数m的值为 ![]() 时,函数F(x)过点A(1,m)的切线至少有2条
时,函数F(x)过点A(1,m)的切线至少有2条
【解析】(Ⅰ)求出f(x)的导数,解关于导函数的不等式,求出函数的单调区间即可;(Ⅱ)求出f(x)的导数,通过讨论a的范围求出函数的单调区间,结合已知条件求出a的范围即可;(Ⅲ)求出函数的导数,求出B处的切线方程,根据函数的单调性求出a的范围即可.
【考点精析】认真审题,首先需要了解利用导数研究函数的单调性(一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减),还要掌握函数的极值与导数(求函数
在这个区间单调递减),还要掌握函数的极值与导数(求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值)的相关知识才是答题的关键.
是极小值)的相关知识才是答题的关键.


科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(2sin
=(2sin ![]() ,2sin
,2sin ![]() ),
), ![]() =(cos
=(cos ![]() ,﹣
,﹣ ![]() sin
sin ![]() ). (Ⅰ)求函数f(x)=
). (Ⅰ)求函数f(x)= ![]()
![]() +
+ ![]() 的最小正周期;
的最小正周期;
(Ⅱ)若β= ![]() ,g(β)=tan2α,α≠
,g(β)=tan2α,α≠ ![]() +
+ ![]() 且α≠
且α≠ ![]() +kπ(k∈Z),数列{an}满足a1=
+kπ(k∈Z),数列{an}满足a1= ![]() ,an+12=
,an+12= ![]() ang(an)(n≤16且n∈N*),令bn=
ang(an)(n≤16且n∈N*),令bn= ![]() ,求数列{bn}的通项公式及前n项和Sn .
,求数列{bn}的通项公式及前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高三共有900名学生,高三模拟考之后,为了了解学生学习情况,用分层抽样方法从中抽出若干学生此次数学成绩,按成绩分组,制成如下的频率分布表:
组号 | 第一组 | 第二组 | 第二组 | 第四组 |
分组 | [70,80) | [80,90) | [90,100) | [100,110) |
频数 | 6 | 4 | 22 | 20 |
频率 | 0.06 | 0.04 | 0.22 | 0.20 |
组号 | 第五组 | 第六组 | 第七组 | 第八组 |
分组 | [110,120) | [120,130) | [130,140) | [140,150] |
频数 | 18 | a | 10 | 5 |
频率 | b | 0.15 | 0.10 | 0.05 |
(1)若频数的总和为c,试求a,b,c的值;
(2)为了了解数学成绩在120分以上的学生的心理状态,现决定在第六、七、八组中用分层抽样方法抽取6名学生,在这6名学生中又再随机抽取2名与心理老师面谈,令第七组被抽中的学生数为随机变量ξ,求随机变量ξ的分布列和数学期望;
(3)估计该校本次考试的数学平均分.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() (其中e是自然对数的底数,a∈R). (Ⅰ)若曲线f(x)在x=l处的切线与x轴不平行,求a的值;
(其中e是自然对数的底数,a∈R). (Ⅰ)若曲线f(x)在x=l处的切线与x轴不平行,求a的值;
(Ⅱ)若函数f(x)在区间(0,1]上是单调函数,求a的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:函数y=log0.5(x2+2x+a)的值域R,命题q:函数y=x2a﹣5在(0,+∞)上是减函数.若p或q为真命题,p且q为假命题,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)在R上可导,其导函数为f′(x),且函数y=(1﹣x)f′(x)的图象如图所示,则下列结论中一定成立的是( ) 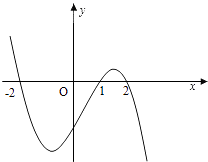
A.函数f(x)有极大值f(2)和极小值f(1)
B.函数f(x)有极大值f(﹣2)和极小值f(1)
C.函数f(x)有极大值f(2)和极小值f(﹣2)
D.函数f(x)有极大值f(﹣2)和极小值f(2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了得到 ![]() 函数的图象,只需把y=3sinx上所有的点( )
函数的图象,只需把y=3sinx上所有的点( )
A.先把横坐标缩短到原来的 ![]() 倍,然后向左平移
倍,然后向左平移 ![]() 个单位
个单位
B.先把横坐标缩短到原来的2倍,然后向左平移 ![]() 个单位
个单位
C.先把横坐标缩短到原来的2倍,然后向左右移 ![]() 个单位
个单位
D.先把横坐标缩短到原来的 ![]() 倍,然后向右平移
倍,然后向右平移 ![]() 个单位
个单位
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以直角坐标系的原点O为极点,x轴的正半轴为极轴,且两个坐标系取相同的单位长度,已知直线I的参数方程为 ![]() (t为参数),圆C的极坐标方程为ρ=2,点P关于极点对称的点P'QUOTE p的极坐标为
(t为参数),圆C的极坐标方程为ρ=2,点P关于极点对称的点P'QUOTE p的极坐标为 ![]()
(1)写出圆C的直角坐标方程及点P的极坐标;
(2)设直线I与圆C相交于两点A、B,求点P到A、B两点的距离之积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】血药浓度(Plasma Concentration)是指药物吸收后在血浆内的总浓度.药物在人体内发挥治疗作用时,该药物的血药浓度应介于最低有效浓度和最低中毒浓度之间.已知成人单次服用1单位某药物后,体内血药浓度及相关信息如图所示: 
根据图中提供的信息,下列关于成人使用该药物的说法中,不正确的个数是( )
①首次服用该药物1单位约10分钟后,药物发挥治疗作用
②每次服用该药物1单位,两次服药间隔小于2小时,一定会产生药物中毒
③每间隔5.5小时服用该药物1单位,可使药物持续发挥治疗作用
④首次服用该药物1单位3小时后,再次服用该药物1单位,不会发生药物中毒.
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com