
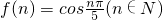 ,则
,则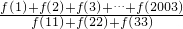 的值为
的值为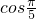

 +cos
+cos )+(cos
)+(cos +cos
+cos )=-(cos
)=-(cos +cos
+cos )+(cos
)+(cos +cos
+cos )=0,然后再利用诱导公式及周期性求解.
)=0,然后再利用诱导公式及周期性求解. +cos
+cos )+(cos
)+(cos +cos
+cos )
) +cos
+cos )+(cos
)+(cos +cos
+cos )=0,f(5)=cosπ=-1;
)=0,f(5)=cosπ=-1; )+cos(π+
)+cos(π+ )+cos(π+
)+cos(π+ )+cos(π+
)+cos(π+ )
) +cos
+cos +cos
+cos +cos
+cos )
)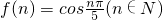 的周期T=
的周期T=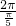 =10,因此从f(1)起,每连续10项的和等于0,
=10,因此从f(1)起,每连续10项的和等于0, +cos
+cos +cos
+cos =cos
=cos
 +cos
+cos +cos
+cos =cos
=cos


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com