
如图,将边长为2的正方形ABCD沿对角线BD折叠,使的平面ABD⊥平面CBD,AE⊥平面ABD,且AE=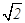 ,
,

(1) 求证:DE⊥AC
(2)求DE与平面BEC所成角的正弦值
(3)直线BE上是否存在一点M,使得CM//平面ADE,若存在,求M的位置,不存在,请说明理由。
(1)以A为原点,以射线AB,AC,AE为坐标轴建立空间直角坐标系,
则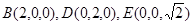 由C作平面ABD的垂线,垂足为F,则F为BC的中点,
由C作平面ABD的垂线,垂足为F,则F为BC的中点,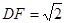 ,所以点C的坐标为
,所以点C的坐标为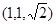 ,
,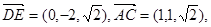
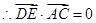
故:DE⊥AC(2)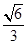 (3)存在M为BE的中点,使得CM//平面ADE
(3)存在M为BE的中点,使得CM//平面ADE
【解析】
试题分析:以A为原点,以射线AB,AC,AE为坐标轴建立空间直角坐标系,
则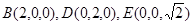
由C作平面ABD的垂线,垂足为F,则F为BC的中点,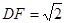 ,
,
所以点C的坐标为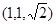 。
。
(1)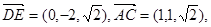
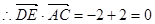 ,故:DE⊥AC。
,故:DE⊥AC。
(2)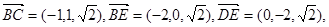
设平面BCE的法向量为 ,则
,则 ,
,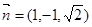
设线面角为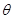 ,
,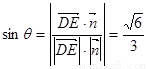
(3)设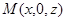 ,则
,则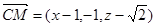 。若CM//平面ADE,则
。若CM//平面ADE,则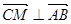 ,所以
,所以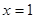 ,故存在M为BE的中点,使得CM//平面ADE。
,故存在M为BE的中点,使得CM//平面ADE。
考点:空间线面平行的判定及性质,线面所成角的求解
点评:采用空间向量的方法求解立体几何问题的步骤:建立空间直角坐标系,写出相关点及相关向量的坐标,将坐标代入证明或计算求解的对应公式求解,空间向量法要求学生数据处理时认真仔细


科目:高中数学 来源: 题型:
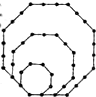 (2012•芜湖三模)如图,将边长为1,2,3的正八边形叠放在一起,同一边上相邻珠子的距离为1,若以此方式再放置边长为4,5,6,…,10的正八边形,则这10个正八边形镶嵌的珠子总数是
(2012•芜湖三模)如图,将边长为1,2,3的正八边形叠放在一起,同一边上相邻珠子的距离为1,若以此方式再放置边长为4,5,6,…,10的正八边形,则这10个正八边形镶嵌的珠子总数是查看答案和解析>>
科目:高中数学 来源: 题型:
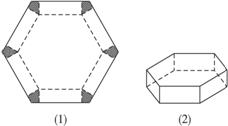
09年湖北鄂州5月模拟文)(12分)如图所示,将边长为2的正三角形铁皮的三个角各切去一个全等的四边形,再沿虚线折起,做成一个无盖的正三棱柱容器,要求正三棱柱容器的高x与底面边长之比不超过正常数t.
⑴把正三棱柱容器的容积V表示为x的函数,并写出函数的定义域;
⑵x为何值时,容积V最大?并求最大值.

查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2010-2011年福建省高二第二学期导数及其运用数学理卷 题型:填空题
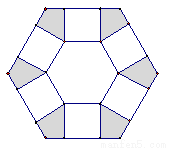
如图,将边长为2的正六边形铁皮的六个角各剪去一个全等四边形,再折起做一个无盖正六棱柱容器,其容积最大时,底面边长为.
查看答案和解析>>
科目:高中数学 来源: 题型:
![]()
图1 图2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com