A
分析:对点B分类讨论,利用椭圆、双曲线、圆的定义即可判断出答案.
解答:对定点B分类讨论:

①若点B在圆A内(不与圆心A重合),如图所示:设点P是圆A上的任意一点,连接PB,作线段PB的垂直平分线l交AP于点M,连接BM,则|AM|+|BM|=|AP|=R>|AB|.
由椭圆的定义可知:点M的轨迹是以点A、B为焦点的椭圆.
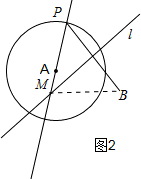
②若点B在圆A外,如图2所示:设点P是圆A上的任意一点,连接PB,作线段PB的垂直平分线l交AP于点M,连接BM,则|BM|-|AM|=|AP|=R<|AB|.
由双曲线的定义可知:点M的轨迹是以点A、B为焦点的双曲线的一支.
③
若定点B与圆心A重合,如图3所示:

设点P是圆A上的任意一点,取线段AP的中点M,则点M满足条件,
因此点M的轨迹是以点A为圆心,以
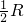
为半径的圆.
④若点B在圆A上,则满足条件的点是一个点B.
综上可知:可以看到满足条件的点M的轨迹可以是:椭圆、双曲线的一支,圆,一个点,而不可能是一条直线.
故选A.
点评:熟练掌握利用椭圆、双曲线、圆的定义、分类讨论的思想方法是解题的关键.


 若定点B与圆心A重合,如图3所示:
若定点B与圆心A重合,如图3所示: 设点P是圆A上的任意一点,取线段AP的中点M,则点M满足条件,
设点P是圆A上的任意一点,取线段AP的中点M,则点M满足条件,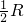 为半径的圆.
为半径的圆.

 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案