分析:(1)把点
(,an+1)代入二次函数解析式,整理后得到数列{a
n}是等差数列,并求出公差,则其通项公式可求.在把数列{a
n}的通项公式代入
bn+1=bn+3an,整理后得到数列{b
n}的递推式,利用类加法求{b
n}的通项公式;
(2)把数列{a
n}、{b
n}的通项公式代入c
n=2a
nb
n,整理后先分组,然后利用错位相减法求和.
解答:解:(1)∵点
(,an+1)在函数y=x
2+1的图象上,
∴
an+1=()2+1,即a
n+1-a
n=1.
∴数列{a
n}是以a
1=1为首项,以1为公差的等差数列.
则a
n=1+1×(n-1)=n.
∴
bn+1=bn+3an=bn+3n,
bn+1-bn=3n.
又b
1=0.
∴当n≥2时,
b
n=b
1+(b
2-b
1)+(b
3-b
2)+…+(b
n-b
n-1)=0+3+3
2+3
3+…+3
n-1=
=-.
此时对n=1时成立.
∴
bn=-;
(2)由c
n=2a
nb
n=2n(
-)=n•3
n-3n.
∴
Sn=(1•31+2•32+…+n•3n)-3(1+2+3+…+n)=
(1•31+2•32+…+n•3n)-.
令
Tn=1•31+2•32+…+n•3n①
3Tn=1•32+2•33+…+(n-1)•3n+n•3n+1②
①-②得:
-2Tn=3+32+…+3n-n•3n+1.
∴
Tn=.
∴
Sn=-.
点评:本题考查了数列的函数特性,考查了等差关系的确定和等差数列的通项公式,等比关系的确定和等比数列的通项公式,训练了分组求和及错位相减法求和,是中档题.



 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案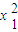 +
+ +…+
+…+ ,B=x1x2+x2x3+…+xn-1xn+xnx1其中x1,x2,…xn都是正数,则A≤B;
,B=x1x2+x2x3+…+xn-1xn+xnx1其中x1,x2,…xn都是正数,则A≤B; +
+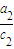 +
+ 的最小值为3;
的最小值为3; +
+ +…+
+…+ +
+ 的最小值为
的最小值为 .
.