
如图,P1(x1,y1),P2(x2,y2),…,Pn(xn,yn)(0<y1<y2<…<yn)是曲线C:y2=3x(y≥0)上的n个点,点Ai(ai,0)(i=1,2,3,…,n)在x轴的正半轴上,且△Ai-1AiPi是正三角形(A0是坐标原点).

(1)写出a1,a2,a3;
(2)求出点An(an,0)(n∈N*)的横坐标an关于n的表达式.
(1)a1=2,a2=6,a3=12(2)an=n(n+1)(n∈N*)
【解析】(1)a1=2,a2=6,a3=12;
(2)依题意,得xn=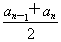 ,yn=
,yn=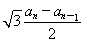 ,由此及
,由此及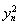 =3xn得
=3xn得 2=
2=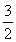 (an-1+an),即(an-an-1)2=2(an-1+an).
(an-1+an),即(an-an-1)2=2(an-1+an).
由(1)可猜想:an=n(n+1)(n∈N*).
下面用数学归纳法予以证明:
(1)当n=1时,命题显然成立;
(2)假定当n=k时命题成立,即有ak=k(k+1),
则当n=k+1时,由归纳假设及(ak+1-ak)2=2(ak+ak+1)得[ak+1-k(k+1)]2=2[k(k+1)+ak+1],
即(ak+1)2-2(k2+k+1)ak+1+[k(k-1)]·[(k+1)(k+2)]=0,
解之得ak+1=(k+1)(k+2)(ak+1=k(k-1)<ak不合题意,舍去),
即当n=k+1时,命题也成立.所以an=n(n+1)(n∈N*).


科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用3练习卷(解析版) 题型:解答题
已知函数f(x)= ax3-
ax3- x2+cx+d(a,c,d∈R)满足f(0)=0,f′(1)=0,且f′(x)≥0在R上恒成立.
x2+cx+d(a,c,d∈R)满足f(0)=0,f′(1)=0,且f′(x)≥0在R上恒成立.
(1)求a,c,d的值;
(2)若h(x)= x2-bx+
x2-bx+ -
- ,解不等式f′(x)+h(x)<0.
,解不等式f′(x)+h(x)<0.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用20练习卷(解析版) 题型:解答题
如图,在直三棱柱ABC ?A1B1C1中,AC=4,CB=2,AA1=2,∠ACB=60°,E、F分别是A1C1,BC的中点.

(1)证明:平面AEB⊥平面BB1C1C;
(2)证明:C1F∥平面ABE;
(3)设P是BE的中点,求三棱锥P ?B1C1F的体积.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用1练习卷(解析版) 题型:填空题
已知函数y=log2(ax-1)在(1,2)上单调递增,则a的取值范围为________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用19练习卷(解析版) 题型:解答题
.已知矩阵A= ,A的一个特征值λ=2,其对应的特征向量是α1=
,A的一个特征值λ=2,其对应的特征向量是α1= .设向量β=
.设向量β= ,试计算A5β的值.
,试计算A5β的值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用17练习卷(解析版) 题型:解答题
为拉动经济增长,某市决定新建一批基础设施工程、民生工程和产业建设工程三类,这三类工程所含项目个数分别占总数的 ,
, ,
, ,现在3名工人独立地从中任意一个项目参与建设.
,现在3名工人独立地从中任意一个项目参与建设.
(1)求他们选择的项目所属类别互不相同的概率.
(2)记X为3人中选择的项目所属于基础设施工程或产业建设工程的人数,求X的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用16练习卷(解析版) 题型:解答题
在四棱锥P-ABCD中,底面ABCD是边长为1的正方形,且PA⊥平面ABCD.

(1)求证:PC⊥BD;
(2)过直线BD且垂直于直线PC的平面交PC于点E,且三棱锥E-BCD的体积取到最大值.
①求此时四棱锥E-ABCD的高;
②求二面角A-DE-B的正弦值的大小.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用13练习卷(解析版) 题型:解答题
已知椭圆的焦点坐标为F1(-1,0),F2(1,0),过F2垂直于长轴的直线交椭圆于P,Q两点,且|PQ|=3.
(1)求椭圆的方程;
(2)过F2的直线l与椭圆交于不同的两点M,N,则△F1MN的内切圆的面积是否存在最大值?若存在,求出这个最大值及此时的直线方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用10练习卷(解析版) 题型:填空题
已知各项都为正的等比数列{an}满足a7=a6+2a5,存在两项am,an使得 =4a1,则
=4a1,则 的最小值为________.
的最小值为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com