【答案】
分析:根据椭圆的标准方程,算出a=3且b=2.再利用椭圆的定义可得|AF
1|+|AF
2|=|BF
1|+|BF
2|=2a=6,因此将△ABF
2的周长分解为(|AF
1|+|AF
2|)+(|BF
1|+|BF
2|),即可得到本题答案.
解答: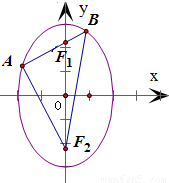
解:∵椭圆的标准方程为
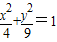
,
∴椭圆的焦点在y轴上,a
2=9,b
2=4,可得a=3且b=2
根据椭圆的定义,得|AF
1|+|AF
2|=|BF
1|+|BF
2|=2a=6
∴△ABF
2的周长为
|AB|+|AF
2|+|BF
2|=(|AF
1|+|AF
2|)+(|BF
1|+|BF
2|)=12
故选:A
点评:本题给出经过椭圆一个焦点的弦与另一个焦点构成的三角形,求该三角形的周长,着重考查了椭圆的标准方程和简单几何性质等知识,属于基础题.

 的焦点F1的弦,F2为另一个焦点,则△ABF2的周长为( )
的焦点F1的弦,F2为另一个焦点,则△ABF2的周长为( ) 解:∵椭圆的标准方程为
解:∵椭圆的标准方程为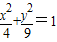 ,
,
