
若直线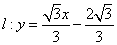 过双曲线
过双曲线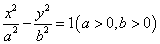 的一个焦点,且与双曲线的一条渐近线平行.
的一个焦点,且与双曲线的一条渐近线平行.
(Ⅰ)求双曲线的方程;
(Ⅱ)若过点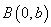 与
与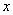 轴不平行的直线与双曲线相交于不同的两点
轴不平行的直线与双曲线相交于不同的两点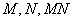 的垂直平分线为
的垂直平分线为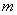 ,求直线
,求直线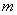 在
在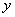 轴上截距的取值范围.
轴上截距的取值范围.
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:高中数学 来源:2014届海南琼海嘉积中学高二上教学监测(三)文科数学试卷(解析版) 题型:选择题
过双曲线的一个焦点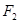 作垂直于实轴的直线,交双曲线于P、Q,
作垂直于实轴的直线,交双曲线于P、Q,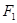 是另一焦点,若∠
是另一焦点,若∠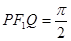 ,则双曲线的离心率
,则双曲线的离心率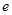 等于( )
等于( )
A.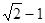 B.
B.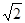 C.
C.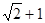 D.
D.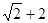
查看答案和解析>>
科目:高中数学 来源:2012-2013学年江苏省高二10月阶段性检测数学试卷(解析版) 题型:填空题
给出下列命题,其中正确命题的序号是 (填序号)。
(1)已知椭圆 两焦点为
两焦点为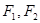 ,则椭圆上存在六个不同点
,则椭圆上存在六个不同点 ,使得
,使得 为直角三角形;
为直角三角形;
(2)已知直线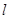 过抛物线
过抛物线 的焦点,且与这条抛物线交于
的焦点,且与这条抛物线交于 两点,则
两点,则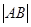 的最小值为2;
的最小值为2;
(3)若过双曲线 的一个焦点作它的一条渐近线的垂线,垂足为
的一个焦点作它的一条渐近线的垂线,垂足为 ,
, 为坐标原点,则
为坐标原点,则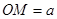 ;
;
(4)已知⊙ ⊙
⊙ 则这两圆恰有2条公切线。
则这两圆恰有2条公切线。
查看答案和解析>>
科目:高中数学 来源:2013届山东冠县武训高中高二下第二次模块考试理科数学试卷(解析版) 题型:选择题
给出下列命题:
①已知椭圆 两焦点
两焦点 ,则椭圆上存在六个不同点
,则椭圆上存在六个不同点 ,使得△
,使得△ 为直角三角形;
为直角三角形;
②已知直线 过抛物线
过抛物线 的焦点,且与这条抛物线交于
的焦点,且与这条抛物线交于 两点,则
两点,则 的最小值为2;
的最小值为2;
③若过双曲线 的一个焦点作它的一条渐近线的垂线,垂足为
的一个焦点作它的一条渐近线的垂线,垂足为 为坐标原点,则
为坐标原点,则 ;
;
④根据气象记录,知道荆门和襄阳两地一年中雨天所占的概率分别为20%和18%,两地同时下雨的概率为12%,则荆门为雨天时,襄阳也为雨天的概率是60%.
其中正确命题的序号是( )
A.①③④ B.①②③ C.③④ D.①②④
查看答案和解析>>
科目:高中数学 来源:福建省长泰一中09-10学年高二下学期期中考(理) 题型:选择题
过双曲线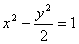 的一个焦点作直线交双曲线于A、B两点,若|AB|=4,则这样的直线有( )
的一个焦点作直线交双曲线于A、B两点,若|AB|=4,则这样的直线有( )
A. 4条 B. 3条 C. 2条 D. 1条
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com