2．下列说法错误的是（　　）

	A．	设有一个回归方程为$\widehat{y}$=3-5x，则变量x每增加一个单位，y平均增加5个单位
	B．	回归直线$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$必过点（$\overline{x}$，$\overline{y}$）
	C．	在一个2×2列联表中，由计算得随机变量K2的观测值k=13.079，则可以在犯错误的概率不超过0.001的前提下，认为这两个变量间有关系
	D．	将一组数据中的每个数据都加上或减去同一个常数后，方差恒不变

1．已知函数f（x）=e^x-alnx的定义域是（0，+∞），关于函数f（x）给出下列命题：
①对于任意a∈（0，+∞），函数f（x）存在最小值；
②对于任意a∈（-∞，0），函数f（x）是（0，+∞）上的减函数；
③存在a∈（-∞，0），使得对于任意的x∈（0，+∞），都有f（x）＞0成立；
④存在a∈（0，+∞），使得函数f（x）有两个零点．
其中正确命题的序号是①④．

20．观察下列各式：

照此规律，当n∈N^*时，C_2n-1⁰+C_2n-1¹+C_2n-1²+…+C_2n-1^n-1=（　　）

A．

4n+1

B．

4n

C．

4n-1

D．

4n-2

19．在极坐标系中，直线ρcosθ=1与圆ρ=2cosθ的位置关系是（　　）

A．

相离

B．

相切

C．

相交但不过圆心

D．

相交且过圆心

18．如图1是一个边长为1的正三角形，分别连接这个三角形三边中点，将在三角剖分成4个三角开（如图2），再分别连接图2中一个小三角形三边的中点，又可将原三角形剖分成7个三角形（如图3），…，依此类推，设第n个图中原三角形被剖分成a_n个三角形，则第4个图中最小三角形的边长为（　　）；a₁₀₀=（　　）

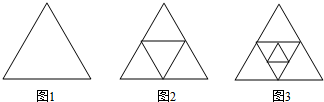
A．

$\frac{1}{6}$，300

B．

$\frac{1}{8}$，300

C．

$\frac{1}{6}$，298

D．

$\frac{1}{8}$，298

17．下面有五个命题：
①函数y=sin⁴x-cos⁴x的最小正周期是π；
②终边在y轴上的角的集合是{α|α=$\frac{kπ}{2}$，k∈Z}；
③函数f（x）=|sin（x+$\frac{π}{3}$）|（x∈R），在区间[$\frac{2π}{3}$，$\frac{7π}{6}$]上是增函数；
④若动直线x=a与函数f（x）=sinx和g（x）=cosx的图象分别交于M，N两点，则|MN|的最大值为1．
其中真命题的序号是①③．

16．投掷一枚均匀硬币，则正面或反面出现的概率都是$\frac{1}{2}$，反复这样的投掷，数列{a_n}定义如下：a_n=$\left\{\begin{array}{l}{1\\ 第n此投掷出现正面}\\{-1\\ 第n此投掷出现反面}\end{array}\right.$，设S_n=a₁+a₂+…a_n，则S₂≠0，且S₆=0的概率为$\frac{1}{8}$．

15．已知数列{a_n}、{b_n}、{c_n}的通项公式分别为：a_n=n，b_n=n（n+1），c_n=n（n+1）（n+2），数列{a_n}，{b_n}的前n项和分别为S₁（n），S₂（n），观察下表：

n	1	2	3	4	5	6	7	8	…
an	1	2	3	4	5	6	7	8	…
S1（n）	1	3	6	10	15	21	28	36	…
bn	2	6	12	20	30	42	56	72	…

发现S₁（n）=$\frac{1}{2}$b_n，并可用下面方法证明：
因为a_k=k=$\frac{1}{2}[k（k+1）-（k-1）k]$，k=1，2，…n，
所以S₁（n）=a₁+a₂+…a_n=1+2+…+n=$\frac{1}{2}{（1×2-0×1）+（2×3-1×2）…+[n（n+1）-（n-1）n]}$=$\frac{1}{2}n（n+1）=\frac{1}{2}{b}_{n}$．
（1）指出S₂（n）与c_n的关系，并类比上面方法证明你的结论；
（2）求和T_n=1²+2²+…+n²．

14．设函数f（x）=x²+aln（x+1）．
（1）若a=-12，写出函数f（x）的单调区间；
（2）若函数f（x）在[2，+∞）上单调递增，求实数a的取值范围；
（3）若在区间[0，1]上，函数f（x）在x=0处取得最大值，求实数a的取值范围．

13．设函数f（x）=-x³+2x²-x（x∈R）．
（1）求曲线y=f（x）在点（2，f（2））处的切线方程；
（2）求函数f（x）的极值．