
科目: 来源: 题型:
【题目】我国古代数学名著《数书九章》中有“天池盆测雨”题:在下雨时,用一个圆台形的天池盆接雨水.天池盆盆口直径为二尺八寸,盆底直径为一尺二寸,盆深一尺八寸.若盆中积水深九寸,则平地降雨量是( )
(注:①平地降雨量等于盆中积水体积除以盆口面积;②一尺等于十寸;③台体的体积公式V= ![]() )
)
A.2寸
B.3寸
C.4寸
D.5寸
查看答案和解析>>
科目: 来源: 题型:
【题目】一个袋中有大小相同,编号分别为1,2,3,4,5的五个球,从中有放回地每次取一个球,共取3次,取得三个球的编号之和不小于13的概率为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】已知点M(﹣1,0)和N(1,0),若某直线上存在点P,使得|PM|+|PN|=4,则称该直线为“椭型直线”.现有下列直线:①x﹣2y+6=0;②x﹣y=0;③2x﹣y+1=0;④x+y﹣3=0.其中是“椭型直线”的是( )
A.①③
B.①②
C.②③
D.③④
查看答案和解析>>
科目: 来源: 题型:
【题目】将函数f(x)=sin(2x﹣ ![]() )的图象向右平移
)的图象向右平移 ![]() 个单位后得到函数g(x),则g(x)具有性质( )
个单位后得到函数g(x),则g(x)具有性质( )
A.最大值为1,图象关于直线x= ![]() 对称
对称
B.在(0, ![]() )上单调递减,为奇函数
)上单调递减,为奇函数
C.在(﹣ ![]() ,
, ![]() )上单调递增,为偶函数
)上单调递增,为偶函数
D.周期为π,图象关于点( ![]() ,0)对称
,0)对称
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标系xOy中,以O为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程为ρcosθ=a(a>0),Q为l上一点,以OQ为边作等边三角形OPQ,且O、P、Q三点按逆时针方向排列.
(Ⅰ)当点Q在l上运动时,求点P运动轨迹的直角坐标方程;
(Ⅱ)若曲线C:x2+y2=a2 , 经过伸缩变换 ![]() 得到曲线C′,试判断点P的轨迹与曲线C′是否有交点,如果有,请求出交点的直角坐标,没有则说明理由.
得到曲线C′,试判断点P的轨迹与曲线C′是否有交点,如果有,请求出交点的直角坐标,没有则说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,点F是抛物线τ:x2=2py (p>0)的焦点,点A是抛物线上的定点,且 ![]() =(2,0),点B,C是抛物线上的动点,直线AB,AC斜率分别为k1 , k2 .
=(2,0),点B,C是抛物线上的动点,直线AB,AC斜率分别为k1 , k2 . 
(I)求抛物线τ的方程;
(Ⅱ)若k1﹣k2=2,点D是点B,C处切线的交点,记△BCD的面积为S,证明S为定值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某厂生产不同规格的一种产品,根据检测标准,其合格产品的质量y(g)与尺寸x(mm)之间近似满足关系式y=axb(a,b为大于0的常数).现随机抽取6件合格产品,测得数据如下:
尺寸(mm) | 38 | 48 | 58 | 68 | 78 | 88 |
质量(g) | 16.8 | 18.8 | 20.7 | 22.4 | 24.0 | 25.5 |
对数据作了初步处理,相关统计量的值如表:
|
|
|
|
75.3 | 24.6 | 18.3 | 101.4 |
(Ⅰ)根据所给数据,求y关于x的回归方程;
(Ⅱ)按照某项指标测定,当产品质量与尺寸的比在区间( ![]() ,
, ![]() )内时为优等品.现从抽取的6件合格产品中再任选3件,记ξ为取到优等品的件数,试求随机变量ξ的分布列和期望.
)内时为优等品.现从抽取的6件合格产品中再任选3件,记ξ为取到优等品的件数,试求随机变量ξ的分布列和期望.
附:对于一组数据(v1 , u1),(v2 , u2),…,(vn , un),其回归直线u=α+βv的斜率和截距的最小二乘估计分别为 ![]() =
= 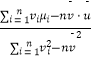 ,
, ![]() =
= ![]() ﹣
﹣ ![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】在如图所示的多面体ABCDEF中,ABCD为直角梯形,AB∥CD,∠DAB=90°,四边形ADEF为等腰梯形,EF∥AD,已知AE⊥EC,AB=AF=EF=2,AD=CD=4.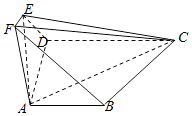
(1)求证:平面ABCD⊥平面ADEF;
(2)求直线CF与平面EAC所成角的正弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知数列{an}满足a1+2a2+…+nan=(n﹣1)2n+1+2,n∈N*
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若bn= ![]() ,Tn=b1+b2+…+bn , 求证:对任意的n∈N* , Tn<
,Tn=b1+b2+…+bn , 求证:对任意的n∈N* , Tn< ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com