
科目: 来源: 题型:
【题目】如图,已知椭圆![]() :
:![]() (
(![]() )的离心率为
)的离心率为![]() ,并以抛物线
,并以抛物线![]() :
:![]() 的焦点
的焦点![]() 为上焦点.直线
为上焦点.直线![]() :
:![]() (
(![]() )交抛物线
)交抛物线![]() 于
于![]() ,
,![]() 两点,分别以
两点,分别以![]() ,
,![]() 为切点作抛物线
为切点作抛物线![]() 的切线,两切线相交于点
的切线,两切线相交于点![]() ,又点
,又点![]() 恰好在椭圆
恰好在椭圆![]() 上.
上.
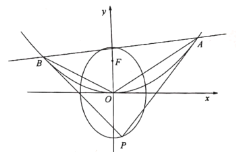
(1)求椭圆![]() 的方程;
的方程;
(2)求![]() 的最大值;
的最大值;
(3)求证:点![]() 恒在
恒在![]() 的外接圆内.
的外接圆内.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() ,满足
,满足![]() ,则( )
,则( )
A.函数![]() 有2个极小值点和1个极大值点
有2个极小值点和1个极大值点
B.函数![]() 有2个极大值点和1个极小值点
有2个极大值点和1个极小值点
C.函数![]() 有可能只有一个零点
有可能只有一个零点
D.有且只有一个实数![]() ,使得函数
,使得函数![]() 有两个零点
有两个零点
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标系中,以原点为极点,x轴的正半轴为极轴建立极坐标系,已知曲线![]() ,直线l的参数方程为:
,直线l的参数方程为:![]() (t为参数),直线l与曲线C分别交于M,N两点.
(t为参数),直线l与曲线C分别交于M,N两点.
(1)写出曲线C和直线l的普通方程;
(2)若点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】工厂质检员从生产线上每半个小时抽取一件产品并对其某个质量指标![]() 进行检测,一共抽取了
进行检测,一共抽取了![]() 件产品,并得到如下统计表.该厂生产的产品在一年内所需的维护次数与指标
件产品,并得到如下统计表.该厂生产的产品在一年内所需的维护次数与指标![]() 有关,具体见下表.
有关,具体见下表.
质量指标 |
|
|
|
频数 |
|
|
|
一年内所需维护次数 |
|
|
|
(1)以每个区间的中点值作为每组指标的代表,用上述样本数据估计该厂产品的质量指标![]() 的平均值(保留两位小数);
的平均值(保留两位小数);
(2)用分层抽样的方法从上述样本中先抽取![]() 件产品,再从
件产品,再从![]() 件产品中随机抽取
件产品中随机抽取![]() 件产品,求这
件产品,求这![]() 件产品的指标
件产品的指标![]() 都在
都在![]() 内的概率;
内的概率;
(3)已知该厂产品的维护费用为![]() 元/次,工厂现推出一项服务:若消费者在购买该厂产品时每件多加
元/次,工厂现推出一项服务:若消费者在购买该厂产品时每件多加![]() 元,该产品即可一年内免费维护一次.将每件产品的购买支出和一年的维护支出之和称为消费费用.假设这
元,该产品即可一年内免费维护一次.将每件产品的购买支出和一年的维护支出之和称为消费费用.假设这![]() 件产品每件都购买该服务,或者每件都不购买该服务,就这两种情况分别计算每件产品的平均消费费用,并以此为决策依据,判断消费者在购买每件产品时是否值得购买这项维护服务?
件产品每件都购买该服务,或者每件都不购买该服务,就这两种情况分别计算每件产品的平均消费费用,并以此为决策依据,判断消费者在购买每件产品时是否值得购买这项维护服务?
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的倾斜角为
的倾斜角为![]() ,且经过点
,且经过点![]() ,以坐标原点O为极点,
,以坐标原点O为极点,![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() ,从原点O作射线交
,从原点O作射线交![]() 于点M,点N为射线OM上的点,满足|
于点M,点N为射线OM上的点,满足| ![]() ,记点N的轨迹为曲线C.
,记点N的轨迹为曲线C.
(1)①设动点![]() ,记
,记![]() 是直线
是直线![]() 的向上方向的单位方向向量,且
的向上方向的单位方向向量,且![]() ,以t为参数求直线
,以t为参数求直线![]() 的参数方程
的参数方程
②求曲线C的极坐标方程并化为直角坐标方程;
(2)设直线![]() 与曲线C交于P,Q两点,求
与曲线C交于P,Q两点,求![]() 的值
的值
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆C:![]() (0<b<2)的离心率为
(0<b<2)的离心率为![]() ,F为椭圆的右焦点,PQ为过中心O的弦.
,F为椭圆的右焦点,PQ为过中心O的弦.
(1)求![]() 面积的最大值;
面积的最大值;
(2)动直线![]() 与椭圆交于A,B两点,证明:在第一象限内存在定点M,使得当直线AM与直线BM的斜率均存在时,其斜率之和是与t无关的常数,并求出所有满足条件的定点M的坐标.
与椭圆交于A,B两点,证明:在第一象限内存在定点M,使得当直线AM与直线BM的斜率均存在时,其斜率之和是与t无关的常数,并求出所有满足条件的定点M的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】水稻是人类重要的粮食作物之一,耕种与食用的历史都相当悠久,日前我国南方农户在播种水稻时一般有直播、撒酒两种方式.为比较在两种不同的播种方式下水稻产量的区别,某市红旗农场于2019年选取了200块农田,分成两组,每组100块,进行试验.其中第一组采用直播的方式进行播种,第二组采用撒播的方式进行播种.得到数据如下表:
产量(单位:斤) 播种方式 | [840,860) | [860,880) | [880,900) | [900,920) | [920,940) |
直播 | 4 | 8 | 18 | 39 | 31 |
散播 | 9 | 19 | 22 | 32 | 18 |
约定亩产超过900斤(含900斤)为“产量高”,否则为“产量低”
(1)请根据以上统计数据估计100块直播农田的平均产量(同一组中的数据用该组区间的中点值为代表)
(2)请根据以上统计数据填写下面的2×2列联表,并判断是否有99%的把握认为“产量高”与“播种方式”有关?
产量高 | 产量低 | 合计 | |
直播 | |||
散播 | |||
合计 |
附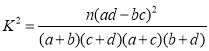 :
:
P(K2≥k0) | 0.10 | 0.010 | 0.001 |
k0 | 2.706 | 6.635 | 10.828 |
查看答案和解析>>
科目: 来源: 题型:
【题目】关于圆周率![]() ,数学发展史上出现过许多很有创意的求法,如著名的蒲丰实验和查理斯实验,受其启发,我们也可以通过设计下面的实验来估计
,数学发展史上出现过许多很有创意的求法,如著名的蒲丰实验和查理斯实验,受其启发,我们也可以通过设计下面的实验来估计![]() 的值:先请240名同学,每人随机写下两个都小于1的正实数x,y组成的实数对
的值:先请240名同学,每人随机写下两个都小于1的正实数x,y组成的实数对![]() ,再统计两数能与1构成钝角三角形三边的数对
,再统计两数能与1构成钝角三角形三边的数对![]() 的个数m;最后再根据计数m来估计π的值.假设统计结果是
的个数m;最后再根据计数m来估计π的值.假设统计结果是![]() ,那么可以估计
,那么可以估计![]() 的近似值为____________.(用分数表示)
的近似值为____________.(用分数表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com