
科目: 来源: 题型:
【题目】在三棱锥P﹣ABC中,平面PBC⊥平面ABC,∠ACB=90°,BC=PC=2,若AC=PB,则三棱锥P﹣ABC体积的最大值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】设椭圆E:![]() +
+![]() =1(a>b>0)的左、右焦点分别为F1,F2,过点F1的直线交椭圆E于A,B两点.若椭圆E的离心率为
=1(a>b>0)的左、右焦点分别为F1,F2,过点F1的直线交椭圆E于A,B两点.若椭圆E的离心率为![]() ,三角形ABF2的周长为4
,三角形ABF2的周长为4![]() .
.
(1)求椭圆E的方程;
(2)设不经过椭圆的中心而平行于弦AB的直线交椭圆E于点C,D,设弦AB,CD的中点分别为M,N,证明:O,M,N三点共线.
查看答案和解析>>
科目: 来源: 题型:
【题目】李先生家住![]() 小区,他工作在
小区,他工作在![]() 科技园区,从家开车到公司上班路上有
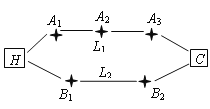
科技园区,从家开车到公司上班路上有![]() 两条路线(如图),
两条路线(如图),![]() 路线上有
路线上有![]() 三个路口,各路口遇到红灯的概率均为
三个路口,各路口遇到红灯的概率均为![]() ;
;![]() 路线上有
路线上有![]() 两个路口,各路口遇到红灯的概率依次为
两个路口,各路口遇到红灯的概率依次为![]() .
.
(Ⅰ)若走![]() 路线,求最多遇到1次红灯的概率;
路线,求最多遇到1次红灯的概率;
(Ⅱ)若走![]() 路线,求遇到红灯次数
路线,求遇到红灯次数![]() 的数学期望;
的数学期望;
(Ⅲ)按照“平均遇到红灯次数最少”的要求,请你帮助李先生从上述两条路线中选择一条最好的上班路线,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,底面ABCD是矩形,侧面PAD⊥底面ABCD,E为PA的中点,过C,D,E三点的平面与PB交于点F,且PA=PD=AB=2.
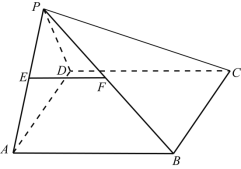
(1)证明:![]() ;
;
(2)若四棱锥![]() 的体积为
的体积为![]() ,则在线段
,则在线段![]() 上是否存在点G,使得二面角
上是否存在点G,使得二面角![]() 的余弦值为
的余弦值为![]() ?若存在,求
?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() .
.
(1)求函数f(x)在[0,π]上的单调递减区间;
(2)在锐角△ABC的内角A,B,C所对边为a,b,c,已知f(A)=﹣1,a=2,求△ABC的面积的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某企业生产甲、乙两种产品均需用A,B两种原料,已知生产1吨每种产品所需原料及每天原料的可用限额如表所示.如果生产1吨甲、乙产品可获利润分别为3万元、4万元,则该企业每天可获得的最大利润为( )
甲 | 乙 | 原料限额 | |
A/吨 | 3 | 2 | 12 |
B/吨 | 1 | 2 | 8 |
A.15万元B.16万元C.17万元D.18万元
查看答案和解析>>
科目: 来源: 题型:
【题目】历史上有不少数学家都对圆周率作过研究,第一个用科学方法寻求圆周率数值的人是阿基米德,他用圆内接和外切正多边形的周长确定圆周长的上下界,开创了圆周率计算的几何方法,而中国数学家刘徽只用圆内接正多边形就求得![]() 的近似值,他的方法被后人称为割圆术.近代无穷乘积式、无穷连分数、无穷级数等各种
的近似值,他的方法被后人称为割圆术.近代无穷乘积式、无穷连分数、无穷级数等各种![]() 值的表达式纷纷出现,使得
值的表达式纷纷出现,使得![]() 值的计算精度也迅速增加.华理斯在1655年求出一个公式:
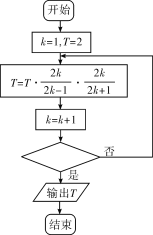
值的计算精度也迅速增加.华理斯在1655年求出一个公式:![]() ,根据该公式绘制出了估计圆周率
,根据该公式绘制出了估计圆周率![]() 的近似值的程序框图,如下图所示,执行该程序框图,已知输出的
的近似值的程序框图,如下图所示,执行该程序框图,已知输出的![]() ,若判断框内填入的条件为
,若判断框内填入的条件为![]() ,则正整数
,则正整数![]() 的最小值是
的最小值是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() ,
,![]() .以坐标原点为极点,
.以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,已知曲线
轴正半轴为极轴建立极坐标系,已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,点
,点![]() 为
为![]() 上的动点,
上的动点,![]() 为
为![]() 的中点.
的中点.
(1)请求出![]() 点轨迹
点轨迹![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() 的极坐标为
的极坐标为![]() 若直线
若直线![]() 经过点
经过点![]() 且与曲线
且与曲线![]() 交于点
交于点![]() ,弦
,弦![]() 的中点为
的中点为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com