
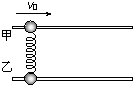
 如图所示,两根位于同一竖直平面内足够长的水平光滑长杆,上、下两杆上分别套着质量相等的甲、乙两金属球,两球之间用一轻质弹簧相连.开始时乙在甲的正下方,且弹簧刚好无弹力.现给甲一个水平向右的初速度v0,此后两球可在杆上无摩擦地滑动.下列叙述中正确的是( )
如图所示,两根位于同一竖直平面内足够长的水平光滑长杆,上、下两杆上分别套着质量相等的甲、乙两金属球,两球之间用一轻质弹簧相连.开始时乙在甲的正下方,且弹簧刚好无弹力.现给甲一个水平向右的初速度v0,此后两球可在杆上无摩擦地滑动.下列叙述中正确的是( )| A、甲、乙两球的动量之和保持不变 | B、甲、乙两球的动能之和保持不变 | C、当甲球的速度为零时,乙球刚好位于甲球的正下方 | D、甲球的速度从v0减小至零的过程中,弹簧的弹性势能先增大后减小 |


科目:高中物理 来源: 题型:
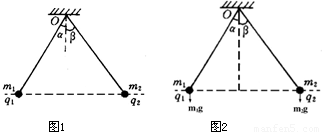
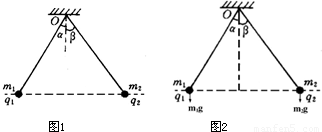
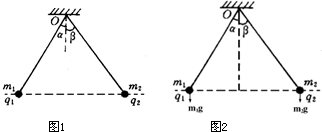 辨析题:如图所示,两个质量分别为m1、m2,带电量分别为q1、q2的金属小球,用两根绝缘轻绳悬挂于同一点O.平衡时,两球恰好位于同一水平面上.轻绳与竖直方向夹角分别为α、β,请确定金属小球质量m1、m2与夹角α、β的关系式.
辨析题:如图所示,两个质量分别为m1、m2,带电量分别为q1、q2的金属小球,用两根绝缘轻绳悬挂于同一点O.平衡时,两球恰好位于同一水平面上.轻绳与竖直方向夹角分别为α、β,请确定金属小球质量m1、m2与夹角α、β的关系式.| m1 |
| m2 |
| sinβ |
| sina |
查看答案和解析>>
科目:高中物理 来源:2000-2008年高考物理试题分类汇编 题型:021
如图所示,两根足够长的固定平行金属光滑导轨位于同水平面,导轨上横放着两根相同的导体棒
ab、cd与导轨构成矩形回路.导体棒的两端连接着处于压缩状态的两根轻质弹簧,两棒的中间用细线绑住,它们的电阻均为R,回路上其余部分的电阻不计.在导轨平面内两导轨间有一竖直向下的匀强磁场.开始时,导体棒处于静止状态.剪断细线后,导体棒在运动过程中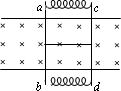
回路中有感应电动势
B.两根导体棒所受安培力的方向相同
C.两根导体棒和弹簧构成的系统动量守恒,机械能守恒
D.两根导体棒和弹簧构成的系统动量守恒,机械能不守恒
查看答案和解析>>
科目:高中物理 来源:上海模拟 题型:问答题
| m1 |
| m2 |
| sinβ |
| sina |
查看答案和解析>>
科目:高中物理 来源:2009年上海市黄浦区高考物理二模试卷(解析版) 题型:解答题
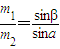
查看答案和解析>>
科目:高中物理 来源:2011-2012学年上海市六校高三(上)第一次联考物理试卷(解析版) 题型:解答题
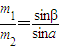
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com