
 如图,物块质量为m,固定在物块上方的轻弹簧劲度为k1,固定在物块下方的轻弹簧劲度k2,下方的轻弹簧另一端与地面固定,当物块静止时,用力拉着上方弹簧的上端A点沿竖直方向缓慢移动一段距离后,恰使下方弹簧的弹力为$\frac{1}{3}mg$,则该段距离可能是( )
如图,物块质量为m,固定在物块上方的轻弹簧劲度为k1,固定在物块下方的轻弹簧劲度k2,下方的轻弹簧另一端与地面固定,当物块静止时,用力拉着上方弹簧的上端A点沿竖直方向缓慢移动一段距离后,恰使下方弹簧的弹力为$\frac{1}{3}mg$,则该段距离可能是( )| A. | $\frac{mg}{3}(\frac{1}{k_1}+\frac{1}{k_2})$ | B. | $\frac{2}{3}mg(\frac{1}{k_1}+\frac{1}{k_2})$ | C. | $\frac{4}{3}mg(\frac{1}{k_1}+\frac{1}{k_2})$ | D. | $\frac{5}{3}mg(\frac{1}{k_1}+\frac{1}{k_2})$ |
分析 题中要求弹簧k2产生的弹力大小变成为$\frac{1}{3}mg$,此时弹簧k2有两种可能的状态:拉伸和压缩.k2原来处于压缩状态,后来处于拉伸或压缩状态,根据胡克定律分别求出k2原来压缩量和后来的伸长量或压缩量,即可得到物体上移的距离.再根据胡克定律求出k1的伸长量,加上物体上移的距离就是A端上移的距离.
解答 解:弹簧k2原先处于压缩状态,压缩量为:x1=$\frac{mg}{{k}_{2}}$,弹簧k1无形变.要使下方弹簧的弹力为$\frac{1}{3}mg$,有两种情况:
情况一:用手拉住弹簧A的上端,缓慢上移时,弹簧k2仍处于压缩状态,压缩量:
x2=$\frac{\frac{1}{3}mg}{{k}_{2}}$=$\frac{mg}{3{k}_{2}}$;
则物体上升的距离为:
S1=x1-x2=$\frac{2mg}{3{k}_{2}}$;
由物体受力平衡可知,弹簧k2处于拉伸状态,伸长量:
x3=$\frac{\frac{2}{3}mg}{{k}_{1}}$=$\frac{2mg}{3{k}_{1}}$
则A的上端应上移为:l1=S1+x3=$\frac{2}{3}mg(\frac{1}{{k}_{1}}+\frac{1}{{k}_{2}})$;
情况二:用手拉住弹簧A的上端,缓慢上移时,弹簧k2处于拉伸状态,伸长量:
x2=$\frac{mg}{3{k}_{2}}$;
则物体上升的距离为:
S2=x1+x2=$\frac{4mg}{3{k}_{2}}$
由物体受力平衡可知,弹簧k1处于拉伸状态,伸长量:
x4=$\frac{\frac{4}{3}mg}{{k}_{1}}$=$\frac{4mg}{3{k}_{1}}$
则A的上端应上移:
l2=S2+x4=$\frac{4mg}{3}$($\frac{1}{{k}_{1}}+\frac{1}{{k}_{2}}$)
故选:BC.
点评 本题的解题关键是分析弹簧的状态,分析出A端上移的距离与弹簧形变量的关系,要注意不能漏解.


科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
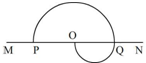 如图,MN为铝质薄平板,铝板上方和下方分别有垂直于图平面的匀强磁场(未画出).一带电粒子从紧贴铝板上表面的P点垂直于铝板向上射出,从Q点穿越铝板后到达PQ的中点O.已知粒子穿越铝板时,其动能损失四分之三,电荷量损失一半,速度方向不变.不计重力.铝板上方和下方的磁感应强度大小之比为( )
如图,MN为铝质薄平板,铝板上方和下方分别有垂直于图平面的匀强磁场(未画出).一带电粒子从紧贴铝板上表面的P点垂直于铝板向上射出,从Q点穿越铝板后到达PQ的中点O.已知粒子穿越铝板时,其动能损失四分之三,电荷量损失一半,速度方向不变.不计重力.铝板上方和下方的磁感应强度大小之比为( )| A. | 2 | B. | $\sqrt{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
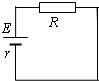
| A. | E | B. | $\frac{E}{R+r}$r | C. | $\frac{E}{R+r}$R | D. | $\frac{E}{r}$R |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | $\frac{8H}{{{{({T_2}-{T_1})}^2}}}$ | B. | $\frac{H}{{4{{({T_2}-{T_1})}^2}}}$ | C. | $\frac{4H}{T_2^2-T_1^2}$ | D. | $\frac{8H}{T_2^2-T_1^2}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 研究和观察日食时,可把太阳当作质点 | |
| B. | 因为子弹的质量、体积都很小,所以在研究子弹穿过一张薄纸所需的时间时,可以把子弹看做质点 | |
| C. | 如果不计空气阻力,则苹果落地的速度比树叶落地的速度大 | |
| D. | “神舟九号”的发射时间是2012年6月16日18点37分,在物理学上是时刻 |
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
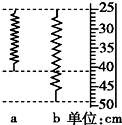 在探究“弹力与弹簧伸长的关系实验”中,弹簧不受力时的长度如图a所示,当在弹簧下挂重2N的钩码时如图b所示.对此下列说法中正确的是D.
在探究“弹力与弹簧伸长的关系实验”中,弹簧不受力时的长度如图a所示,当在弹簧下挂重2N的钩码时如图b所示.对此下列说法中正确的是D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com