Question

8．在如图所示的匀强电场中，长为L的绝缘细线一端系于O点，另一端系一带正电的小球，小球的电荷量$q=\frac{{\sqrt{3}mg}}{3E}$．  求：
（1）细线拉直小球从OA水平位置由静止释放到速度第一次为零时细线与过O点竖直线的夹角，此时小球位置的电势．（以过O点的等势面为零等势面）
（2）从A点释放后小球的最大速度．
（3）若细线拉直小球从OB水平位置的B点由静止释放．问：小球上升的高度．
①若在OA下方或恰到OA线上，说明理由；
②若能到达OA上方求出经过OA线时的速度大小．

Answer 1

分析 （1）应用动能定理求出细线与竖直方向的夹角，然后求出电势；
（2）由动能定理可以求出小球的最大速度；
（3）应用动能定理求出小球到达最高点时的速度．

解答 解：（1）设与竖直线夹角为θ，
由动能定理得：mglcosθ-qE（l+lsinθ）=0-0，
整理得：$\frac{cosθ}{1+sniθ}=\frac{{\sqrt{3}}}{3}$；
由半角公式：$\frac{cosθ}{1+sniθ}=\frac{{sni（{{90}^0}-θ）}}{{1+cos（{{90}^0}-θ）}}=tan\frac{{（{{90}^0}-θ）}}{2}=\frac{{\sqrt{3}}}{3}$$\frac{{（{{90}^0}-θ）}}{2}={30^0}$，
解得：θ=30⁰，（或直接把$\frac{cosθ}{1+sniθ}=\frac{{\sqrt{3}}}{3}$变形解得   θ=30⁰均可）
电势：φ=ELsin30°=$\frac{1}{2}$EL；
（2）有对称性当细绳从水平摆过60⁰角时速度最大
由动能定理得：$mgLsin{60^0}-qE（L-Lcos{60^0}）=\frac{1}{2}m{v^2}$，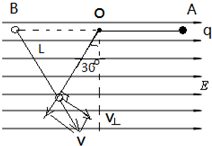
解得：$v=\sqrt{\frac{{2\sqrt{3}}}{3}gL}$；
（3）能到达OA线以上．
从B点释放到细线刚被拉直小球在合力作用下作直线运动．
刚拉直时由动能定理：${F_合}=\frac{mg}{{cos{{30}^0}}}$${F_合}•L=\frac{mg}{{cos{{30}^0}}}L=\frac{1}{2}m{v^2}$
拉直后与线垂直的速度为（拉直时损失能量）：${v_⊥}=vcos{30^0}$
此后到OA线由动能定理得：$qE（Lsni{30^0}+L）-mgLcos{30^0}=\frac{1}{2}mv_{OA}^2-\frac{1}{2}mv_⊥^2$，
解得：${v_{OA}}=\sqrt{\sqrt{3}gL}$；
答：（1）此时小球位置的电势为$\frac{1}{2}$EL．
（2）从A点释放后小球的最大速度为$\sqrt{\frac{2\sqrt{3}}{3}gL}$．
（3）①能到达OA线以上；②经过OA线时的速度大小为$\sqrt{\sqrt{3}gL}$．

点评 本题是一道力学综合题，难度较大，分析清楚运动过程是正确解题的关键，应用动能定理可以解题，解题时注意小球做圆周运动的临界条件．