
 如图所示,一物体由静止开始,从A点出发分别沿三个倾斜角不同但高度相同的粗糙斜面滑下,并分别从B、C、D三点滑至同一水平面上.三个斜面及水平面的动摩擦因数均相同,三个斜面并排放置,互不影响,斜面与水平面之间由很小一段曲面平滑连接,则( )
如图所示,一物体由静止开始,从A点出发分别沿三个倾斜角不同但高度相同的粗糙斜面滑下,并分别从B、C、D三点滑至同一水平面上.三个斜面及水平面的动摩擦因数均相同,三个斜面并排放置,互不影响,斜面与水平面之间由很小一段曲面平滑连接,则( )| A. | 物体运动到B、C、D三点时,动能相等 | |
| B. | 物体运动到B、C、D三点时,重力的瞬时功率相等 | |
| C. | 物体在斜面上下滑的过程,其中沿AD斜面下滑重力的平均功率最大 | |
| D. | 物体从A点开始运动到最终停在水平面的过程中,全过程运动的水平距离相等 |
分析 根据受力分析求得摩擦力,进而得到摩擦力做的功,从而由动能定理求得动能,进而得到竖直分速度,然后求得重力的瞬时功率;根据匀变速运动规律求得运动时间进而求得重力平均功率;
根据动能定理求解得到水平位移.
解答 解:A、设A点到水平面的高度为好,斜面倾斜角为θ,那么摩擦力为μmgcosθ,所以,摩擦力做功${W}_{f}=-f\frac{h}{sinθ}=-μmghcotθ$;
又有物体下滑过程只有重力、摩擦力做功,故由动能定理可得滑到底端时的动能Ek=mgh-μmghcotθ,所以,物体运动到B、C、D三点时,动能不相等,故A错误;
B、物体滑到底端的速度$v=\sqrt{2gh(1-μcotθ)}$,那么,速度的竖直分量vy=vsinθ随θ变化而变化,又有重力的瞬时功率P=mgvy,故物体运动到B、C、D三点时,重力的瞬时功率不相等,故B错误;
C、物体在斜面上下滑的过程重力做功相同;物体下滑时合外力为mgsinθ-μmgcosθ,故加速度a=g(sinθ-μcosθ),下滑位移为$\frac{h}{sinθ}$,故运动时间$t=\sqrt{\frac{2×\frac{h}{sinθ}}{g(sinθ-μcosθ)}}=\sqrt{\frac{2h}{g}•\frac{1}{sinθ(sinθ-μcosθ)}}$,故θ越大,t越小,故沿AD斜面下滑的时间最长,重力的平均功率最小,故C错误;
D、设物体在水平面上滑行s,那么,由物体运动过程只有重力摩擦力做功应用动能定理可得:mgh-μmghcotθ-μmgs=0,所以,$hcotθ+s=\frac{h}{μ}$,即全过程运动的水平距离相等,故D正确;
故选:D.
点评 经典力学问题一般先对物体进行受力分析,求得合外力及运动过程做功情况,然后根据牛顿定律、动能定理及几何关系求解.


科目:高中物理 来源: 题型:多选题
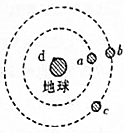 如图所示,a、b、c是圆形轨道上运动的3颗卫星,其中b、c是两颗同步卫星,d是地球赤道上随地球自转的物体,下列说法正确的是( )
如图所示,a、b、c是圆形轨道上运动的3颗卫星,其中b、c是两颗同步卫星,d是地球赤道上随地球自转的物体,下列说法正确的是( )| A. | b、c向心加速度大小相等,向心力大小也相等 | |
| B. | d随地球自转的角速度与b、c角速度的相等,但d的向心加速度大小比b、c的小 | |
| C. | c加速可追上同一轨道上的b,b减速可等候同一轨道上的c | |
| D. | a卫星由于稀薄空气的阻力的影响,轨道半径缓慢减小,则其线速度将增大,机械能将减小 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 正电荷只在电场力作用下,一定从高电势向低电势运动 | |
| B. | 在一个点电荷形成的电场中没有场强相同的两点,但有电势相等的两点 | |
| C. | 电势为零处,场强不一定为零;但场强为零处,电势一定为零 | |
| D. | 初速为零的正电荷在电场力作用下不一定沿电场线运动 |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
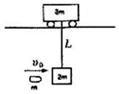 如图所示,质量为3m的小车静止在光滑水平轨道上,下面用长为L的细线悬挂着质量为2m的沙箱,一颗质量为m的子弹以v0的水平速度射入沙箱,并留在其中,在以后运动过程中,求:沙箱上升到最高点时的速度.
如图所示,质量为3m的小车静止在光滑水平轨道上,下面用长为L的细线悬挂着质量为2m的沙箱,一颗质量为m的子弹以v0的水平速度射入沙箱,并留在其中,在以后运动过程中,求:沙箱上升到最高点时的速度.查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 爱因斯坦提出了相对性原理光速不变原理 | |
| B. | 牛顿提出了太阳系行星运动三大定律 | |
| C. | 卡文迪许发现了万有引力定律 | |
| D. | 伽利略认为物体的运动需要力来维持 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
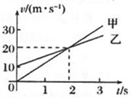 甲、乙两车在平直公路上同向行驶,其v-t图象如图所示.已知两车在t=2s时并排行驶,则( )
甲、乙两车在平直公路上同向行驶,其v-t图象如图所示.已知两车在t=2s时并排行驶,则( )| A. | 甲车和乙车从同一地点出发 | B. | 在t=0时,甲车在乙车前10m | ||
| C. | 甲车的加速度小于乙车的加速度 | D. | 甲、乙车只相遇一次 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
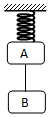 如图,轻质弹簧下挂重为300N的物体A时伸长了3cm,再挂上重为200N的物体B时又伸长了2cm,现将AB间的细线烧断,使A在竖直平面内振动,则( )
如图,轻质弹簧下挂重为300N的物体A时伸长了3cm,再挂上重为200N的物体B时又伸长了2cm,现将AB间的细线烧断,使A在竖直平面内振动,则( )| A. | 最大回复力为300N,振幅为2cm | |
| B. | 最大回复力为200N,振幅为3cm | |
| C. | 只减小A的质量,振动的振幅变小,周期不变 | |
| D. | 只减小B的质量,振动的振幅变小,周期不变 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | α粒子散射实验可以估算出原子核半径的数量级是10-10m | |
| B. | 氢原子的能级理论是在玻尔在卢瑟福核式结构模型的基础上提出来的 | |
| C. | 汤姆孙通过对阴极射线的研究提出了原子核具有复杂的结构 | |
| D. | 卢瑟福的α粒子散射实验揭示了原子只能处于一系列不连续的能量状态中 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com