
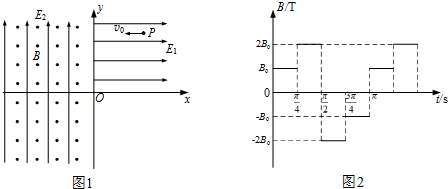
���� ��1������������Һ����x��0������������ֱ���µ�������ˮƽ���ҵĵ糡�������ã�Һ������ֱ�����������������˶�����ˮƽ���������ȼ����˶����г���Ӧ���˶�ѧ�ķ��̼��ɣ�
��2���ṩ���������Եõ�����뾶���ɹ���뾶�ɵ����ڣ��ɴų��ı仯���Ի����ڵ�һ��ʱ�������ӵ��˶��켣�����˶��켣�ļ��ι�ϵ�ɵõ������˶���ʱ�䣮
��3�����ݵڶ��ʵõ��Ľ�������Եõ��ڵڶ��������͵���ʱ����ڵ��˶��켣����ͼ�м��ι�ϵ������˶�ѧ�Ĺ�ʽ���ɣ�
��� �⣺��1��Һ����x��0������������ֱ���µ�������ˮƽ���ҵĵ糡�������ã�
Һ������ֱ�����������������˶���
$y=\frac{1}{2}g{t}^{2}$
v=gt
��ã�v=4m/s
Һ����ˮƽ���������ȼ����˶�
v0=at E1q=ma
E1=1.875N/C
��2��Һ�ν���x��0����������� E2q=mg��Һ���˶��켣��ͼ1��ʾ������Բ���˶��Ĵ�СԲ�뾶�ֱ�Ϊr1��r2���˶����ڷֱ�ΪT1��T2����
qvB0=$\frac{m{v}^{2}}{{r}_{1}}$
2 qvB0=$\frac{m{v}^{2}}{{r}_{2}}$
r1=2 m r2=1 m
${T}_{1}=\frac{2��m}{q{B}_{0}}$��${T}_{2}=\frac{��m}{q{B}_{0}}$
����T1=�� s T2=$\frac{��}{2}$s
Һ�δ�P�㵽�ڶ��δ���x�ᾭ����ʱ��t����
${t}_{��}=t+\frac{{T}_{1}}{4}+\frac{{T}_{2}}{2}=��\frac{��}{2}+0.4��$ s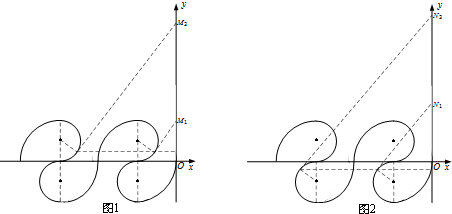
��3������һ�����ų���ʧʱ��Һ����x���Ϸ�����ͼ1��ʾ��
OM1=$\frac{{r}_{1}-{r}_{2}cos30��}{tan30��}+{r}_{2}��1-sin30�㣩$=$2\sqrt{3}-1$ m
OM2=$\frac{3{r}_{1}-{r}_{2}cos30��}{tan30��}+{r}_{2}��1-sin30�㣩$=$6\sqrt{3}-1$m
���������Կɵã�Һ�δ���y��ʱ������yn���㣺
yn=$\frac{{��2n-1��r}_{1}-{r}_{2}cos30��}{tan30��}+{r}_{2}��1-sin30�㣩$
yn=$2\sqrt{3}��2n-1��-1$ m ��ʽ��n=1��2��3��������
���ζ������ų���ʧʱ��Һ����x���·�����ͼ2��ʾ��
ON1=$\frac{{r}_{1}+{r}_{2}cos30��}{tan30��}-{r}_{2}��1-sin30�㣩$=$2\sqrt{3}+1$m
ON2=$\frac{3{r}_{1}+{r}_{2}cos30��}{tan30��}-{r}_{2}��1-sin30�㣩$=$6\sqrt{3}+1$ m
���������Կɵã�Һ�δ���y��ʱ������yn���㣺
yn=$\frac{��2n-1��{r}_{1}+{r}_{2}cos30��}{tan30��}-{r}_{2}��1-sin30�㣩$
yn=[$2\sqrt{3}��2n-1��+1$]m ��ʽ��n=1��2��3��������
�𣺣�1���糡ǿ����1.875N/C��Һ�ε���O��ʱ�ٶ�v�Ĵ�С��4m/s��
��2��Һ�δ�P�㿪ʼ�˶����ڶ��ξ���x�������ʱ����$��\frac{��}{2}+0.4��$s��
��3������ijʱ����ų�ͻȻ��ʧ������Һ��ǡ������y���������30��ǵķ���y������x��0������Һ�δ���y��ʱ��λ����[$2\sqrt{3}��2n-1��+1$]m ��ʽ��n=1��2��3������
���� �����ص��ǶԴų������Ե�Ӧ�ã��ų���������һ���ͻ��������˶������Եı仯����ֻҪ�õ�һ�����ڵ��˶��켣���Ϳ����ظ����켣��ֱ���õ���Ҫ�Ľ���������������ӵ��˶��켣�Ƚϸ��ӣ��ʿ�����Ѷ���Խϴ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ�ѡ����

| A�� | �պϵ���Ժ�һֱ���ֱպ�״̬ | |
| B�� | �պϵ���Ժ��ٶϿ����˲�� | |
| C�� | �Ͽ�����Ժ��ó���ȦA����о˲�� | |
| D�� | �Ͽ����ʹ�������Ļ���ͷ�����ƶ� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
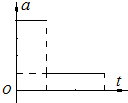 һ������һ���ij��ٶȴ�һ�̶�б��ĵ����ϳ壬��б����ijһ��صˣ�б��ֲڣ������˶������м��ٶ���ʱ���ϵͼ����ͼ��ʾ�������ķ�ͼ��ֱ��ʾ�����˶�������λ��x���ٶ�v������Ek����������Ep����б���Ϊ�ο�ƽ�棩��ʱ��仯�Ĺ�ϵͼ��������ȷ���ǣ�������
һ������һ���ij��ٶȴ�һ�̶�б��ĵ����ϳ壬��б����ijһ��صˣ�б��ֲڣ������˶������м��ٶ���ʱ���ϵͼ����ͼ��ʾ�������ķ�ͼ��ֱ��ʾ�����˶�������λ��x���ٶ�v������Ek����������Ep����б���Ϊ�ο�ƽ�棩��ʱ��仯�Ĺ�ϵͼ��������ȷ���ǣ�������| A�� | 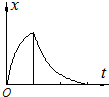 | B�� | 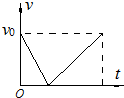 | C�� |  | D�� | 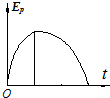 |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
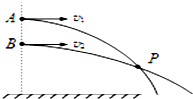 ��ͼ��ʾ����ͬһ��ֱ���ϲ�ͬ�߶�A��B���㴦���ֱ�������v1��v2ͬ��ˮƽ�׳�����С��PΪ�����˶��켣�Ľ��㣮������˵����ȷ���У�������
��ͼ��ʾ����ͬһ��ֱ���ϲ�ͬ�߶�A��B���㴦���ֱ�������v1��v2ͬ��ˮƽ�׳�����С��PΪ�����˶��켣�Ľ��㣮������˵����ȷ���У�������| A�� | ������P��һ��������ͬ������ | |
| B�� | ��ͬʱ�׳�����������P������ | |
| C�� | ��ͬʱ�׳������ǰ������ֱ����ľ������ | |
| D�� | ��ͬʱ�׳������ǰ����֮��ľ������ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | ��λʱ�����ݳ��Ĺ������ | B�� | �����ֹ��ѹ | ||
| C�� | ������� | D�� | ����ӵ��������� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
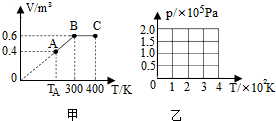 ��ͼ����һ��������������״̬A����״̬B��Ϊ״̬C��V-Tͼ����֪������״̬Aʱ��ѹǿ��1.5��105Pa��
��ͼ����һ��������������״̬A����״̬B��Ϊ״̬C��V-Tͼ����֪������״̬Aʱ��ѹǿ��1.5��105Pa���鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
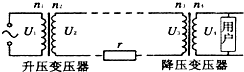 ��ͼΪԶ�������ʾ��ͼ��������������ѹU1������ߵĵ��衢�����ѹ�����������䣬��n1��n2=n4��n3�����û����ĵĹ�������ʱ�����б�����ȷ���ǣ�������
��ͼΪԶ�������ʾ��ͼ��������������ѹU1������ߵĵ��衢�����ѹ�����������䣬��n1��n2=n4��n3�����û����ĵĹ�������ʱ�����б�����ȷ���ǣ�������| A�� | �û��ĵ�ѹU4���� | B�� | ����U1��U2=U4��U3 | ||
| C�� | ���������ĵĹ��ʼ�С | D�� | �������������ʲ��� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
 ��ͼ��ʾ��U�ι��ҹܺ�����Ϊ��ܺ�������2�������������ˮ�����һ�γ�Ϊ30cm���¶�Ϊ577.5K�Ŀ���������������ˮ����߶Ȳ�Ϊ21cm��������ѹΪ76cmHg��������ܵķ�����彵�£�ʹ�����������ȱ�Ϊ20cm����
��ͼ��ʾ��U�ι��ҹܺ�����Ϊ��ܺ�������2�������������ˮ�����һ�γ�Ϊ30cm���¶�Ϊ577.5K�Ŀ���������������ˮ����߶Ȳ�Ϊ21cm��������ѹΪ76cmHg��������ܵķ�����彵�£�ʹ�����������ȱ�Ϊ20cm�����鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
 ��ͼ��ʾ��һ��������Ϊ2kg���Գ��ٶ�V0=3m/s��б��A�㴦�»�������б��Ħ����Ϊ8N������B���ѹ������20cm��ֹͣ��Ȼ���ֱ����أ��ɵľ���ϵ��������ܻص��ĸ߶ȣ�
��ͼ��ʾ��һ��������Ϊ2kg���Գ��ٶ�V0=3m/s��б��A�㴦�»�������б��Ħ����Ϊ8N������B���ѹ������20cm��ֹͣ��Ȼ���ֱ����أ��ɵľ���ϵ��������ܻص��ĸ߶ȣ��鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com