
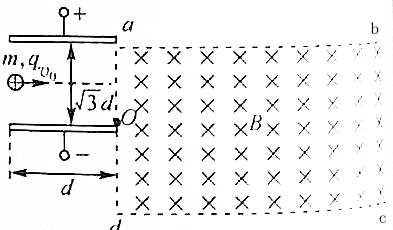
分析 (1)粒子在电场中做类似平抛运动,根据分位移公式列式求解即可;
(2)对类平抛运动,根据分运动公式列式求解末速度v;进入磁场后做匀速圆周运动,画出临界轨迹,结合几何关系和牛顿第二定律列式分析讨论.
解答 解:(1)粒子做类平抛运动,根据牛顿第二定律,有:
a=$\frac{qU}{m•\sqrt{3}d}$
根据分位移公式,有:
d=v0t
$\frac{\sqrt{3}}{2}d=\frac{1}{2}a{t}^{2}$
联立解得:
U=$\frac{3m{v}_{0}^{2}}{q}$
(2)粒子做类平抛运动,根据分运动公式,有:
vx=v0
vy=at
合速度大小:
v=$\sqrt{{v}_{x}^{2}+{v}_{y}^{2}}$
速度偏转角的正切值为:
tanθ=$\frac{{v}_{y}}{{v}_{x}}$
联立解得:
v=2v0
tanθ=$\sqrt{3}$,故θ=60°
假设磁感应强度从零开始增加,根据公式r=$\frac{mv}{qB}$,轨道半径也就从零开始增加,讨论如下:
临界一:
B=0,做匀速直线运动,从cd边射出,速度偏转角为零;
临界二:
轨道与cd相切,轨迹如图所示:
结合几何关系,有:
sin30°=$\frac{r-\sqrt{3}d}{r}$
解得:r=2$\sqrt{3}$d
速度偏转角等于圆弧的圆心角,为150°;
洛伦兹力提供向心力,故:
$qv{B}_{1}=m\frac{{v}^{2}}{r}$
联立解得:
${B}_{1}=\frac{\sqrt{3}m{v}_{0}}{3qd}$
临界三:
轨迹与ab边相切,如图所示:
结合几何关系,有:
R+Rsin30°=$\sqrt{3}d$
解得:R=$\frac{2}{3}\sqrt{3}d$
速度偏转角等于圆弧的圆心角,为300°;
洛伦兹力提供向心力,故:
$qv{B}_{2}=m\frac{{v}^{2}}{R}$
联立解得:
${B}_{2}=\frac{\sqrt{3}m{v}_{0}}{qd}$
故B≤$\frac{\sqrt{3}m{v}_{0}}{3qd}$时,速度偏转角为60°,从cd边射出;
$\frac{\sqrt{3}m{v}_{0}}{3qd}$<B<$\frac{\sqrt{3}m{v}_{0}}{qd}$时,速度偏转角为150°,从ab边射出;
B≥$\frac{\sqrt{3}m{v}_{0}}{qd}$时,速度偏转角为300°,从ad边射出;
答:(1)两板间的电压U为$\frac{3m{v}_{0}^{2}}{q}$;
(2)当B≤$\frac{\sqrt{3}m{v}_{0}}{3qd}$时,速度偏转角为60°,从cd边射出;
当$\frac{\sqrt{3}m{v}_{0}}{3qd}$<B<$\frac{\sqrt{3}m{v}_{0}}{qd}$时,速度偏转角为150°,从ab边射出;
当B≥$\frac{\sqrt{3}m{v}_{0}}{qd}$时,速度偏转角为300°,从ad边射出.
点评 本题要明确粒子的运动性质,分为类平抛运动和匀速圆周运动过程进行分析,关键是找出临界轨迹,结合几何关系、牛顿第二定律进行分析,不难.


 名校课堂系列答案
名校课堂系列答案科目:高中物理 来源: 题型:解答题
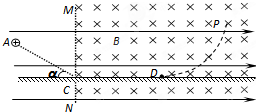 如图所示,空间内存在水平向右的匀强电场,在虚线MN的右侧有垂直纸面向里、磁感应强度为B的匀强磁场,一质量为m、带电荷量为+q的小球自A点由静止开始运动,刚好沿直线AC运动至光滑绝缘的水平面CD点,与水平面碰撞的瞬间,小球的竖直分速度立即减为零,而水平分速度不变,小球运动至D处刚好离开水平面,然后沿图示曲线DP轨迹运动,AC与水平面夹角α=45°,重力加速度为g,求:
如图所示,空间内存在水平向右的匀强电场,在虚线MN的右侧有垂直纸面向里、磁感应强度为B的匀强磁场,一质量为m、带电荷量为+q的小球自A点由静止开始运动,刚好沿直线AC运动至光滑绝缘的水平面CD点,与水平面碰撞的瞬间,小球的竖直分速度立即减为零,而水平分速度不变,小球运动至D处刚好离开水平面,然后沿图示曲线DP轨迹运动,AC与水平面夹角α=45°,重力加速度为g,求:查看答案和解析>>
科目:高中物理 来源: 题型:选择题
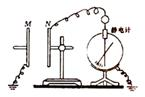 如图所示,由M、N两块相互靠近的平行金属板组成的平行板电容器,极板N与静电计的金属球相接,极板M与静电计的外壳均接地.给电容器充电,静电计指针张开一定角度.以下实验过程中电容器所带电荷量可认为不变,下面操作能使静电计指针张角变大的是( )
如图所示,由M、N两块相互靠近的平行金属板组成的平行板电容器,极板N与静电计的金属球相接,极板M与静电计的外壳均接地.给电容器充电,静电计指针张开一定角度.以下实验过程中电容器所带电荷量可认为不变,下面操作能使静电计指针张角变大的是( )| A. | 在M、N之间插入有机玻璃板 | |
| B. | 将M板沿水平向右方向靠近N板 | |
| C. | 将M板向上平移 | |
| D. | 在M、N之间插入金属板,且不和M、N接触 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
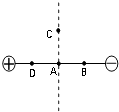 如图,A为等量异种电荷的连线的中点,C是两电荷连线垂直平分线上的点,且AB=AC=AD,则A、B、C、D三点处的场强大小为EA、EB、EC、ED,电势为φA、φB、φC、φD,则下列说法正确的是( )
如图,A为等量异种电荷的连线的中点,C是两电荷连线垂直平分线上的点,且AB=AC=AD,则A、B、C、D三点处的场强大小为EA、EB、EC、ED,电势为φA、φB、φC、φD,则下列说法正确的是( )| A. | EB=ED>EC>EA,φB=φC=φD>φA | |
| B. | EB=ED>EA>EC,φD>φA=φC>φB | |
| C. | 将正的试探电荷q放入该电场中,q在B点的电势能大于在C点的电势能 | |
| D. | 将正的试探电荷q放入该电场中,q在A点的电势能等于在C点的电势能 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
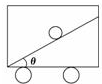 火车正沿水平直线做匀加速运动,在车厢中有一个装置所示,小球与光滑斜面相对静止,斜面与水平面的夹角为θ,根据这一现象判断火车的加速度方向及大小.
火车正沿水平直线做匀加速运动,在车厢中有一个装置所示,小球与光滑斜面相对静止,斜面与水平面的夹角为θ,根据这一现象判断火车的加速度方向及大小.查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,汽车(可视为质点)以8m/s匀速行驶,在即将通过路口时,绿灯还有2s将熄灭,此时汽车距离停车线18m.如果汽车立即做匀加速运动,要求在绿灯熄灭时汽车恰好通过停车线,则:
如图所示,汽车(可视为质点)以8m/s匀速行驶,在即将通过路口时,绿灯还有2s将熄灭,此时汽车距离停车线18m.如果汽车立即做匀加速运动,要求在绿灯熄灭时汽车恰好通过停车线,则:查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,ab和cd是位于水平面内的平行金属轨道,间距为l,其电阻可忽略不计,ac之间连接一阻值为R的电阻.ef为一垂直于ab和cd的金属杆,它与ad和cd接触良好并可沿轨道方向无摩擦地滑动.电阻可忽略.整个装置处在匀强磁场中,磁场方向垂直于图中纸面向里,磁感应强度为B,当施外力使杆ef以速度v向右匀速运动时,杆ef所受的安培力大小为多少?
如图所示,ab和cd是位于水平面内的平行金属轨道,间距为l,其电阻可忽略不计,ac之间连接一阻值为R的电阻.ef为一垂直于ab和cd的金属杆,它与ad和cd接触良好并可沿轨道方向无摩擦地滑动.电阻可忽略.整个装置处在匀强磁场中,磁场方向垂直于图中纸面向里,磁感应强度为B,当施外力使杆ef以速度v向右匀速运动时,杆ef所受的安培力大小为多少?查看答案和解析>>
科目:高中物理 来源: 题型:解答题
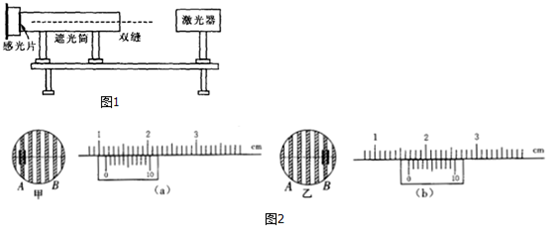
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 如图4所示,一个直径为d的纸质圆筒以角速度ω绕其轴心匀速转动,一子弹沿AO方向打进纸筒,在纸筒转不到半周时,子弹在纸筒上又留下一个弹孔B,已知∠AOB=θ,则子弹速度v为( )
如图4所示,一个直径为d的纸质圆筒以角速度ω绕其轴心匀速转动,一子弹沿AO方向打进纸筒,在纸筒转不到半周时,子弹在纸筒上又留下一个弹孔B,已知∠AOB=θ,则子弹速度v为( )| A. | 2ωd | B. | $\frac{ωd}{2θ}$ | C. | $\frac{ωd}{θ}$ | D. | $\frac{ωd}{(π-θ)}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com