
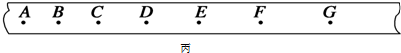
���� ��1���ڡ���֤ţ�ٵڶ����ɵ�ʵ�顱��Ҫע��ƽ��Ħ������ͬʱҪע�����ʵ���ԭ����ʵ�鷽������ʵ���е�ע�����ʵ����ۣ�
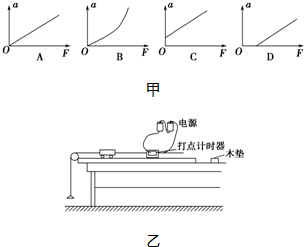
��2����̽�����ٶ������������Ĺ�ϵʱ��Ӧƽ��Ħ������ƽ��Ħ����ʱ���ľ���ù��ߣ�ƽ��Ħ�������ȣ�С���ܵ��ĺ�������������a-Fͼ����a�����нؾࣻ���û��ƽ��Ħ������ƽ��Ħ�������㣬С���ܵ��ĺ���С��������a-Fͼ����F�����нؾ࣮
��3������ʵ��װ�õİ�װ������Ӷ���ȷ���ֵ����Դ���
��4���������������С���ļ��ٶȣ�
��� �⣺��1��A��Ϊ��֤����С����������ɰ��СͰ����������С��Ӧʹɰ��СͰ��������ԶС��С������������������Լ�Сʵ������A��ȷ��
B��С���ļ��ٶ�Ӧͨ������ʱ�������ֽ���������B����
C��������㷨��ͼ��������ʵ�����ݣ��������Լ�С������������ֱ�۵ط�ӳ��������֮��Ĺ�ϵ����C��ȷ��
D��Ϊ�˽�ͼ��������Ϥ��ֱ�ߣ���ֱ�۷�ӳ���������Ĺ�ϵ��a��M�ɷ��ȣ������ݴ���Ӧ��a-M1ͼ��D��ȷ��
��ѡ��ACD��
��2����ƽ��Ħ����ʱ���ѳ�ľ���һ���ù��ߣ�ʹ�����ƫ��С��������ľ�����µķ�������С���ܵ�Ħ������С���ܵ��ĺ�������ɰͰ����������ɰͰ��С��ʩ������ǰ��С���Ѿ��м��ٶȣ���̽������ļ��ٶ������Ĺ�ϵʱ��������a-Fͼ����a�����нؾ࣬��C��ȷ��ABD����
��3����ʵ��ԭ��ͼ��֪������ʱ���õı����ǽ����磬ͼ���õ���ֱ���磻С���ͷŵ�λ��Ӧ�ÿ�����ʱ�����Ա�����������������С��ͬʱľ��ˮƽ��û��ƽ��Ħ������
��4���������֪���м����ĸ���û�л�������T=5��0.02=0.1s��
xAB=4.22cm=0.0422m��xBC=4.65cm=0.0465m��xCD=5.08cm=0.0508m��xDE=5.49cm=0.0549m��xEF=5.91cm=0.0591m��xFG=6.34cm=0.0634m�������������a=$\frac{{x}_{DG}-{x}_{AD}}{9{T}^{2}}$=$\frac{��0.0549+0.0591+0.0634��-��0.0422+0.0465+0.0508��}{9����0.1��^{2}}$=0.42m/s2��
�ʴ�Ϊ����1��ACD ��2��C ��3������ʱ��ʹ��ֱ����Դ��С�������ʱ����ľ���̫����ľ��ˮƽ��û��ƽ��Ħ��������4��0.42
���� ���⿼���ˡ�̽�����ٶ�������������ϵ����ʵ����ע�������Լ�����ͼ�������ݵȻ���֪ʶ��Ҫע���ʵ�飬��ǿ�Ի���ʵ������⣬ͬʱע������������ȷӦ�ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��

| A�� | ��������t=6sʱ�����������˶�����ͨ������λ��Ϊ�� | |
| B�� | ��������t=6sʱ�����˶�����һֱ���䣬��ͨ������λ�ƴ�СΪ4 m | |
| C�� | ��������t=6sʱ�����������˶� | |
| D�� | ��������t=6sʱ�����˶�����һֱ���� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
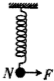 ��ͼ��ʾ��һ��ֱ�ᵯ���϶˹ʶ����¶�ϵ��һС��С����N����ֹ�������ֶ�С��ʩ��һ��ˮƽ��F��ʹ����ƫ�ƣ����ƶ�С��Ĺ����е�������ֱ����ļнǦȣ�90�㣬�ҵ��ɵ��쳤�������������ȣ�С���N����ʼ�����ĸ߶���h��ʾ���������ķ�ͼ�У�����ȷ��ӳ�߶�h��нǦȵ����ҵĺ�����ϵ���ǣ�������
��ͼ��ʾ��һ��ֱ�ᵯ���϶˹ʶ����¶�ϵ��һС��С����N����ֹ�������ֶ�С��ʩ��һ��ˮƽ��F��ʹ����ƫ�ƣ����ƶ�С��Ĺ����е�������ֱ����ļнǦȣ�90�㣬�ҵ��ɵ��쳤�������������ȣ�С���N����ʼ�����ĸ߶���h��ʾ���������ķ�ͼ�У�����ȷ��ӳ�߶�h��нǦȵ����ҵĺ�����ϵ���ǣ�������| A�� |  | B�� | 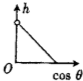 | C�� | 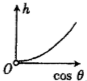 | D�� | 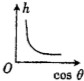 |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�������
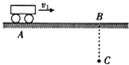 ��ͼ��ʾ��һ�г�Ϊ100m�Ļ���v1=40m/s���ٶ�������ʻ���������������B��200m��A��ʱ��Ħ�г�˾���Ӿ���·60m��C����v2=10m/s���ٶ����������B��ʻ�������ǻĿ��ȣ�Ħ�г�˾����Ħ�г��Ĵ�С���ƣ�����Ħ�г���ֹͣ�����ж�Ħ�г��ܷ�ȫͨ����·���ڣ���ͨ������˵�����ɣ�
��ͼ��ʾ��һ�г�Ϊ100m�Ļ���v1=40m/s���ٶ�������ʻ���������������B��200m��A��ʱ��Ħ�г�˾���Ӿ���·60m��C����v2=10m/s���ٶ����������B��ʻ�������ǻĿ��ȣ�Ħ�г�˾����Ħ�г��Ĵ�С���ƣ�����Ħ�г���ֹͣ�����ж�Ħ�г��ܷ�ȫͨ����·���ڣ���ͨ������˵�����ɣ��鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
 ��ͼ��ʾ��������ȫ��ͬ�Ľ�����a��b�������ǹ̶��ھ�Ե֧���ϣ������ļ�ľ���lΪ��뾶��3������ʹ���Ǵ��ϵ������ֵ�ɣ��������ΪQ��a��b����֮��Ŀ�����F1��������Ϊ��Ե�������������ΪQ���ҵ�ɾ��ȷֲ��������ϣ���ʱa��b����֮��Ŀ�����F2��������
��ͼ��ʾ��������ȫ��ͬ�Ľ�����a��b�������ǹ̶��ھ�Ե֧���ϣ������ļ�ľ���lΪ��뾶��3������ʹ���Ǵ��ϵ������ֵ�ɣ��������ΪQ��a��b����֮��Ŀ�����F1��������Ϊ��Ե�������������ΪQ���ҵ�ɾ��ȷֲ��������ϣ���ʱa��b����֮��Ŀ�����F2��������| A�� | F1=k$\frac{{Q}^{2}}{{l}^{2}}$��F2=k$\frac{{Q}^{2}}{{l}^{2}}$ | B�� | F1��k$\frac{{Q}^{2}}{{l}^{2}}$��F2��k$\frac{{Q}^{2}}{{l}^{2}}$ | ||
| C�� | F1��k$\frac{{Q}^{2}}{{l}^{2}}$��F2=k$\frac{{Q}^{2}}{{l}^{2}}$ | D�� | F1=k$\frac{{Q}^{2}}{{l}^{2}}$��F2��k$\frac{{Q}^{2}}{{l}^{2}}$ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�������
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
 ����ͼ��ʾװ�ÿ����о�Ӱ��ƽ�Ȱ���������ݵ����أ����������������ΪS���������ľ���Ϊd��������ʵĽ�糣��Ϊ?�������ָ��ƫ��Ϊ�ȣ�ʵ���У�����������������䣬
����ͼ��ʾװ�ÿ����о�Ӱ��ƽ�Ȱ���������ݵ����أ����������������ΪS���������ľ���Ϊd��������ʵĽ�糣��Ϊ?�������ָ��ƫ��Ϊ�ȣ�ʵ���У�����������������䣬�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com