Question

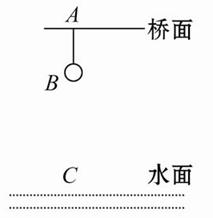
当今流行一种“蹦极”运动，如图所示，在距河面45 m高的桥上A点系弹性绳，另一端B点系住重50 kg男孩的脚，弹性绳原长AB为15 m，设男孩从桥面自由下坠直至紧靠水面的C点，末速度为0。假定整个过程中，弹性绳遵循胡克定律，绳的质量、空气阻力忽略不计，男孩视为质点。弹性势能可用公式E_s=计算，式中k为弹性绳的劲度系数,x为弹性绳的形变长度，g=

10 m/s²。则：

(1)男孩在最低点时，弹性绳具有的弹性势能为多大？弹性绳的劲度系数又为多大？

(2)在整个运动过程中，男孩的最大速度为多少？

Answer 1

【解析】男孩从桥面自由下落到紧靠水面的C点的过程中，重力势能的减少量对应弹性势能的增加量，男孩速度最大时，应位于加速度为零的位置。

(1)由功能转化关系可知，

mgh=E_s                                                                      (2分)

E_s=50×10×45 J=2.25×10⁴ J                                          (1分)

又E_s=kx²,x=45 m-15 m=30 m                                         (2分)

所以                                  (2分)

(2)男孩加速度为零时，mg=kx′                                        (2分)

解得x′=10 m                                                            (1分)

由能量转化和守恒定律得：

                                               (4分)

所以v_m=20 m/s                                                           (2分)

答案：(1)2.25×10⁴ J    50 N/m   (2)20 m/s