

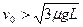
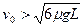
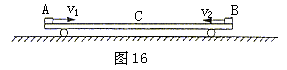
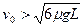 时, 物块B、A在木板C上不可能再发生碰撞
时, 物块B、A在木板C上不可能再发生碰撞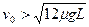
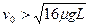
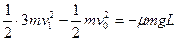 ②
②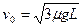
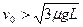
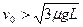 时,A、B将发生碰撞,物块B与档板P发生碰撞的临界情况是:物块B运动到档板P所在处时,B、C的速度相等。同(1)中结论,在临界状况下,当B运动到档板P处时,A、B、C三者速度相等,设此速度为v2,根据动量守恒定律得:
时,A、B将发生碰撞,物块B与档板P发生碰撞的临界情况是:物块B运动到档板P所在处时,B、C的速度相等。同(1)中结论,在临界状况下,当B运动到档板P处时,A、B、C三者速度相等,设此速度为v2,根据动量守恒定律得: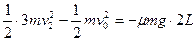 ④
④ 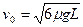
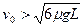
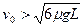 时,B将与档板P相撞,撞后A、B、C的运动可由(2)中运动类比得到:B、P碰撞后瞬间,物块A、B速度相同,木板C速度最大,然后C以较大的加速度向右做减速运动,而物块A和B以相同的较小加速度向右做加速运动,加速过程将持续到或者A、B与C速度相同,三者以相同速度
时,B将与档板P相撞,撞后A、B、C的运动可由(2)中运动类比得到:B、P碰撞后瞬间,物块A、B速度相同,木板C速度最大,然后C以较大的加速度向右做减速运动,而物块A和B以相同的较小加速度向右做加速运动,加速过程将持续到或者A、B与C速度相同,三者以相同速度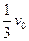 向右做匀速运动,或者木块A从木板C上掉了下来,因此物块B、A在木板C上不可能再发生碰撞。
向右做匀速运动,或者木块A从木板C上掉了下来,因此物块B、A在木板C上不可能再发生碰撞。 3mv3=mv0 ⑤
3mv3=mv0 ⑤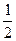 (3m)v32-
(3m)v32-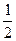 mv02 =-μmg·4L ⑥
mv02 =-μmg·4L ⑥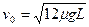
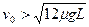
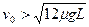 时,A将从木板C上掉下来。设A刚从木板C上掉下来时,A、B、C三者的速度分别为vA″, vB″, vC″,有vA″=vB″<vC″,这时⑤式应改写成
时,A将从木板C上掉下来。设A刚从木板C上掉下来时,A、B、C三者的速度分别为vA″, vB″, vC″,有vA″=vB″<vC″,这时⑤式应改写成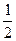 (2m)vB″2+
(2m)vB″2+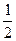 mv″C2-
mv″C2-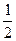 mv0=-μmg·4L ⑧
mv0=-μmg·4L ⑧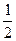 (2m)v42 —
(2m)v42 —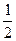 (mv″B2+mvC″2)= -μmgL ⑩
(mv″B2+mvC″2)= -μmgL ⑩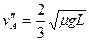 ,
,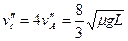 ,
,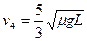


 字词句段篇系列答案
字词句段篇系列答案科目:高中物理 来源:不详 题型:问答题

查看答案和解析>>
科目:高中物理 来源:不详 题型:问答题
查看答案和解析>>
科目:高中物理 来源:不详 题型:问答题

查看答案和解析>>
科目:高中物理 来源:不详 题型:问答题
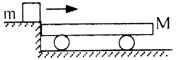
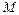 =400g的木块A和B,一质量为
=400g的木块A和B,一质量为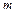 =50g的子弹以水平速度
=50g的子弹以水平速度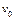 =100m/s射入木块A,当子弹穿出A时,速度
=100m/s射入木块A,当子弹穿出A时,速度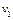 =80m/s,子弹未穿出木块B,若木块与地面间的动摩擦因数均为μ=0.2,求子弹射入B后,B木块在地面上前进的距离.
=80m/s,子弹未穿出木块B,若木块与地面间的动摩擦因数均为μ=0.2,求子弹射入B后,B木块在地面上前进的距离. 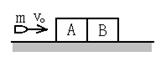
查看答案和解析>>
科目:高中物理 来源:不详 题型:单选题
| A.由于爆炸,系统总动能增大,总动量增大 |
| B.卫星的动量增大,火箭的动量减小,系统动量守恒 |
| C.星箭分离后火箭速度越大,系统的总动能越大 |
| D.若爆炸作用力持续的时间一定,则星箭分离后火箭速度越小,卫星受到的冲击力越大 |
查看答案和解析>>
科目:高中物理 来源:不详 题型:问答题
| A.放射性同位素的衰变快慢可以用人工方法控制 |
| B.同一种物质的原子发光时,只能辐射几种不同频率的光 |
| C.对核能的和平利用不仅能够利用重核裂变,也能利用轻核的聚变现象 |
| D.光子射到金属表面,一定有光电子射出 |
查看答案和解析>>
科目:高中物理 来源:不详 题型:问答题
查看答案和解析>>
科目:高中物理 来源:不详 题型:问答题
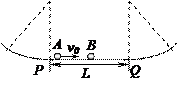
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com