
质量为M的小车,以速度v0在光滑水平地面前进,上面站着一个质量为m的人,问:当人以相对车的速度u向后水平跳出后,车速度为多大?
![]()
错解一:设人跳出后的瞬间车速为v,则其动量为Mv,根据动量守恒定律有:
(M+m)v0=Mv
![]()
错解二:设人跳出后的车速为v,车的动量为Mv,人的动量为m(u+v),根据动量守恒定律有:
(M+m)v0=Mv+m(u+v)
![]()
错解三:设车的前进方向为正方向,人在跳出车后,车的动量为Mv,人的动量为-mu,根据动量守恒定律有:
(M+m)v0=Mv-mu
![]()
错解四:设车的前进方向为正方向,则人跳出车后小车的动量Mv,人的动量为-m(u-v0),根据动量守恒定律有:
(M+m)v0=Mv-m(u-v0)
![]()
错解一的错误原因是动量守恒的对象应为车和人的系统,而错解一中把人跳离车后的动量丢掉了,即以系统的一部分(车)来代替系统(车和人)。
错解二:是没有考虑到,人跳离车前后动量方向的变化。而是简单地采用了算术和,忽略了动量的矢量性。
错解三的错误在于参考系发生变化了。人跳离前人与车的动量是相对地的。人跳离车后车的动量(Mv)也是相对地的,而人跳离车后人的动量(mu)却是相对于车而言的,所以答案不对。
错解四中的错误在于对速度的瞬时性的分析。v0是人未跳离车之前系统(M+m)的速度,-m(u-v0)就不能代表人跳离车后瞬间人的动量。
【正确解答】 选地面为参照系,以小车前进的方向为正方向,根据动量守恒定律有:
(M+m)v0=Mv-m(u-v)
![]()
【小结】 应用动量守恒定律解题时应注意几个方面。
(1)整体性,动量守恒定律是对一个物体系统而言的,具有系统的整体性,而不能对系统的一个部分,如本题错解一。
(2)矢量性,动量守恒是指系统内部各部分动量的矢量和保持不变,在解题时必须运用矢量法则来计算而不能用算术方法,如本题错解二。
(3)相对性,动量守恒定律中系统在作用前后的动量都应是相对于同一惯性参考系而言。如系统的各部分所选取的参考系不同,动量守恒不成立。如本题错解三。
(4) 瞬时性,一般来说,系统内的各部分在不同时刻具有不同的动量,系统在某一时刻的动量,应该是此时刻系统内各部分的瞬时动量的矢量和。


科目:高中物理 来源: 题型:

查看答案和解析>>
科目:高中物理 来源: 题型:
 如图所示,光滑水平面上停放一个木箱和小车,木箱的质量为m,小车和人总的质量为M,M∶m=4∶1, 人以速率v沿水平方向将木箱推出,木箱被挡板以原速反弹回来以后,人接住木箱再以同样大小的速度v第二次推出木箱,木箱又被原速反弹……,问人最多能推几次木箱?
如图所示,光滑水平面上停放一个木箱和小车,木箱的质量为m,小车和人总的质量为M,M∶m=4∶1, 人以速率v沿水平方向将木箱推出,木箱被挡板以原速反弹回来以后,人接住木箱再以同样大小的速度v第二次推出木箱,木箱又被原速反弹……,问人最多能推几次木箱?
查看答案和解析>>
科目:高中物理 来源:2012届辽宁省高二下学期第二次月考物理试题 题型:选择题
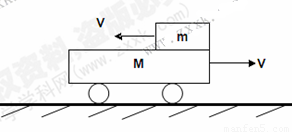
如图所示,在光滑的水平面上,质量M小车正以速度V向右匀速运动,现有一质置为m的木块也以运度V从右端冲向车面,由于摩擦力的作用,小车的速度将发生变化,为使小车继续保持V匀速运动,需及时给小车施加一水平力。当N与m的速度相等时,将力去掉.(已知:m与M的摩擦因数一定,m、V为已知量),
求:(1)从开始到m速速为零的过程中m、M的对地位移之比为多少?
(2)从开始到撤去水平力的过程中水平力对小车做的功为多少?
查看答案和解析>>
科目:高中物理 来源: 题型:
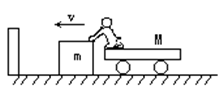
(07年南开区检测)(16分)如图所示,光滑的水平地面上停着一个木箱和小车,木箱质量为m,小车和人的总质量为M,M∶m = 4,人以速率v沿水平方向将木箱推出,木箱被挡板以原速反弹回来以后,人接住木箱再以同样大小的速率v第二次推出木箱,木箱又被原速反弹……问人最多能推几次木箱?
查看答案和解析>>
科目:高中物理 来源:2012-2013学年广东省广州市海珠区高三(上)综合测试物理试卷(二)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com