
 ,管内无空气阻力,取g=10m/s2)求:
,管内无空气阻力,取g=10m/s2)求: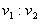 ;
; 。
。 
科目:高中物理 来源: 题型:
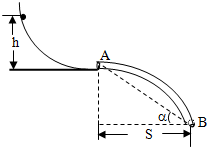 如图所示,AB是根据某平抛运动轨迹制成的内壁光滑的细圆管轨道,轨道上端A与一光滑斜槽的末端水平面相切.已知细圆管轨道的水平长度为S=2.4m;两端口连线与水平方向的夹角α=37°.(取sin37°=0.6,cos37°=0.8,g=10m/s2)求
如图所示,AB是根据某平抛运动轨迹制成的内壁光滑的细圆管轨道,轨道上端A与一光滑斜槽的末端水平面相切.已知细圆管轨道的水平长度为S=2.4m;两端口连线与水平方向的夹角α=37°.(取sin37°=0.6,cos37°=0.8,g=10m/s2)求查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com