
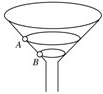
 如图所示,固定的锥形漏斗内壁是光滑的,内壁上有两个质量相等的小球A和B,在各自不同的水平面内做匀速圆周运动,则以下关于线速度v、周期T、向心加速度a及小球对内壁的压力N的关系中正确的是
如图所示,固定的锥形漏斗内壁是光滑的,内壁上有两个质量相等的小球A和B,在各自不同的水平面内做匀速圆周运动,则以下关于线速度v、周期T、向心加速度a及小球对内壁的压力N的关系中正确的是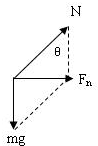 解:设漏斗内壁母线与水平方向的夹角为θ.以任意一个小球为研究对象,分析受力情况:重力mg和漏斗内壁的支持力N,它们的合力提供向心力,如图,则根据牛顿第二定律得
解:设漏斗内壁母线与水平方向的夹角为θ.以任意一个小球为研究对象,分析受力情况:重力mg和漏斗内壁的支持力N,它们的合力提供向心力,如图,则根据牛顿第二定律得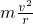 ,得到v=
,得到v= ,θ一定,则v与
,θ一定,则v与 成正比,A球的圆周运动半径大于B球的圆周运动,所以vA>vB.
成正比,A球的圆周运动半径大于B球的圆周运动,所以vA>vB.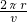 =2π
=2π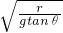 ,T与
,T与 成正比,则TA>TB.
成正比,则TA>TB. ,m,θ相同,则NA=NB.
,m,θ相同,则NA=NB.

科目:高中物理 来源: 题型:
 如图所示,固定的锥形漏斗内壁是光滑的,内壁上有两个质量相等的小球A和B,在各自不同的水平面内做匀速圆周运动,则以下关于线速度v、周期T、向心加速度a及小球对内壁的压力N的关系中正确的是( )
如图所示,固定的锥形漏斗内壁是光滑的,内壁上有两个质量相等的小球A和B,在各自不同的水平面内做匀速圆周运动,则以下关于线速度v、周期T、向心加速度a及小球对内壁的压力N的关系中正确的是( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com