Question

5£®ÈçͼËùʾ£¬ÔÚxÖáÉÏ·½´æÔÚ´¹Ö±xoyƽÃæµÄÔÈÇ¿´Å³¡£¬ÔÚxÖáÏ·½´æÔÚ×ÅÈçͼËùʾµÄÔÈÇ¿µç³¡£®Ò»ÕýµçºÉ´ÓyÖáÉϵÄAµãÑØyÖáÕý·½ÏòÒÔËÙ¶ÈvÉäÈë´Å³¡ÖУ¬OA=a£¬µçºÉÔڴų¡ÖÐ×öÔ²ÖÜÔ˶¯µÄ°ë¾¶Îªr=$\sqrt{2}$a£®µçºÉ´øµçÁ¿Îªq¡¢ÖÊÁ¿Îªm£®£¨ÖØÁ¦²»¼Æ£©Çó£º
£¨1£©´Å¸ÐӦǿ¶È¼°µçºÉ´ÓÉäÈë´Å³¡µ½µÚÒ»´Î¾­¹ýxÖáÓõÄʱ¼ä£»
£¨2£©µçºÉµÚÈý´Î¾­¹ýxÖáʱ¾àOµãµÄ¾àÀ룻
£¨3£©µçºÉµÚËĴξ­¹ýxÖáʱµÄËٶȴóС ¼°ËÙ¶ÈÓëxÖá¼Ð½Ç£®

Answer 1

·ÖÎö £¨1£©Á£×Ó´ÓAµã½øÈë´Å³¡£¬½áºÏÁ£×ÓÔڴų¡Öеİ뾶£¬»­³öÁ£×ÓÔ˶¯µÄ¹ì¼££¬·ÖÎöÁ£×ÓÔڴų¡ÖÐƫתµÄ½Ç¶È£¬È»ºó½áºÏ£º$\frac{¦È}{2¦Ð}=\frac{t}{T}$¼´¿ÉÇó³öÁ£×Ó´ÓÉäÈë´Å³¡µ½µÚÒ»´Î¾­¹ýxÖáÓõÄʱ¼ä£»
£¨2£©Á£×ÓµÚÒ»´Î½øÈëµç³¡ºó×öÔȱäËÙÖ±ÏßÔ˶¯£¬²¢ÇÒÔٴδÓÈëÉäµã·µ»Ø´Å³¡£¬È»ºóÔڴų¡ÖÐ×öÔÈËÙÔ²ÖÜÔ˶¯£¬»­³öÔ˶¯µÄ¹ì¼££¬½áºÏ¼¸ºÎ¹Øϵ¼´¿ÉÇó³öµçºÉµÚÈý´Î¾­¹ýxÖáʱ¾àOµãµÄ¾àÀ룻
£¨3£©Á£×ÓµÚ¶þ´Î½øÈëµç³¡ºó£¬ÓÉÓÚÔ˶¯µÄ·½ÏòÓëµç³¡µÄ·½Ïò´¹Ö±£¬ËùÒÔÁ£×ÓÔڵ糡ÖÐ×öÀàƽÅ×Ô˶¯£¬½«Á£×ÓµÄÔ˶¯·Ö½â¼´¿ÉÇó³ö£®

½â´ð ½â£º£¨1£©Á£×Ó´ÓAµã½øÈë´Å³¡£¬»­³öÁ£×ÓÔ˶¯µÄ¹ì¼£Èçͼ£¬

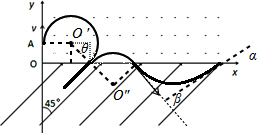
ÆäÖУº$sin¦È=\frac{a}{r}=\frac{a}{\sqrt{2}a}=\frac{\sqrt{2}}{2}$
ËùÒÔ£º¦È=45¡ã
ËùÒÔÁ£×ÓÔڴų¡ÖÐƫתµÄ½Ç¶È ÊÇ£º¦Á=180¡ã+¦È=180¡ã+45¡ã=225¡ã
Á£×ÓÔڴų¡ÖÐÔ˶¯µÄÖÜÆÚ£ºT=$\frac{2¦Ðr}{v}$
ËùÒÔÁ£×ÓÔڴų¡ÖÐÔ˶¯µÄʱ¼ä£º$t=\frac{¦Á}{360¡ã}•T=\frac{225¡ã}{360¡ã}•\frac{2¦Ðr}{v}=\frac{5\sqrt{2}¦Ða}{4v}$
£¨2£©ÓÉÓÚÁ£×ÓÔڴų¡ÖÐƫתµÄ½Ç¶ÈÊÇ225¡ã£¬ËùÒÔÁ£×Ó½«Äæ×ŵ糡Ïߵķ½Ïò½øÈëµç³¡£¬Ôڵ糡ÖÐÏȼõËÙ£¬ºó¼ÓËÙ£¬ÈÔÈ»´Ó½øÈëµç³¡µÄµãÉä³öµç³¡£¬Éä³öµç³¡µÄËÙ¶ÈÈÔÈ»ÊÇv£¬ËùÒÔÁ£×ÓÔڴų¡ÖÐÔ˶¯µÄ°ë¾¶ÈÔÈ»ÊÇr£¬¸ù¾ÝÔ˶¯µÄ¶Ô³ÆÐÔ¿ÉÖª£¬Á£×ÓÔڴų¡Öн«ÔÙ´Îƫת£¬Æ«×ªµÄ½Ç¶ÈÊÇ90¡ã£¬ËùÒÔµçºÉµÚÈý´Î¾­¹ýxÖáʱ¾àOµãµÄ¾àÀ룺
$L=r+r•cos45¡ã+\sqrt{2}r$=$\sqrt{2}a+\frac{\sqrt{2}}{2}¡Á\sqrt{2}a+\sqrt{2}¡Á\sqrt{2}a=£¨3+\sqrt{2}£©a$
£¨3£©½áºÏÔ˶¯µÄ¶Ô³ÆÐÔ¿ÉÖª£¬Á£×ÓµÚ¶þ´Î½øÈëµç³¡ºóËٶȵķ½ÏòÓëxÖáÖ®¼äµÄ¼Ð½ÇÈÔÈ»ÊÇ45¡ã£¬ËùÒÔÁ£×ÓËٶȵķ½ÏòÓëµç³¡µÄ·½Ïò´¹Ö±£¬Á£×ÓÔڵ糡ÖÐ×öÀàƽÅ×Ô˶¯£¬ÓÉÔ˶¯µÄ·Ö½âµÄ֪ʶ¿ÉÖª£¬µ±Á£×ÓµÚËĴε½´ïxÖáʱ£¬ÑØ´¹Ö±Óڵ糡µÄ·½ÏòµÄλÒÆÓëÑص糡·½ÏòµÄλÒÆ´óСÏàµÈ£¬¼´x_¡Î=x_¡Í£®
Ñص糡Ïߵķ½Ïò£º${x}_{¡Î}=\frac{{v}_{¡Í}}{2}t$
ÑØ´¹Ö±Óڵ糡Ïߵķ½Ïò£ºx_¡Í=vt
ËùÒÔ£ºv_¡Í=2v
µçºÉµÚËĴξ­¹ýxÖáʱµÄËٶȴóС£º${v}_{Ä©}=\sqrt{{v}^{2}+{v}_{¡Í}^{2}}=\sqrt{5}v$
Ä©ËÙ¶ÈÓë´¹Ö±Óڵ糡·½ÏòÖ®¼äµÄ¼Ð½Ç£º$tan¦Â=\frac{{v}_{¡Í}}{v}=\frac{2}{1}$
ËÙ¶ÈÓëxÖá¼Ð½Ç£º¦Á=¦Â-45¡ã=arctan2-45¡ã
´ð£º£¨1£©´Å¸ÐӦǿ¶È¼°µçºÉ´ÓÉäÈë´Å³¡µ½µÚÒ»´Î¾­¹ýxÖáÓõÄʱ¼äÊÇ$\frac{5\sqrt{2}¦Ða}{4v}$£»
£¨2£©µçºÉµÚÈý´Î¾­¹ýxÖáʱ¾àOµãµÄ¾àÀëÊÇ$£¨3+\sqrt{2}£©a$£»
£¨3£©µçºÉµÚËĴξ­¹ýxÖáʱµÄËٶȴóСÊÇ$\sqrt{5}v$£¬ËÙ¶ÈÓëxÖá¼Ð½ÇÊÇarctan2-45¡ã£®

µãÆÀ ¸ÃÌ⿼²é´øµçÁ£×ÓÔڴų¡ÖкÍÔڵ糡ÖеÄÔ˶¯£¬´øµçÁ£×ÓÔÚµç´Å³¡ÖеÄÔ˶¯Òª×¢Òâ·ÖÎö¹ý³Ì£¬²¢½áºÏ¸÷¹ý³ÌÖÐÉæ¼°µ½µÄÔ˶¯¹æÂɲÉÓúÏÀíµÄÎïÀí¹æÂÉÇó½â£®