
 如图一根边长为a、b、c(a≥b≥c)的矩形截面长棒,由半导体锑化铟制成.棒中有平行于a边的电流I通过.该棒放在平行于c的外磁场B中,电流I所产生的磁场忽略不计.该电流的载流子为电子,在只有电场存在时,电子在半导体中的平均速度v=μE,(E为沿电流方向的匀强电场场强),其中μ为迁移率.
如图一根边长为a、b、c(a≥b≥c)的矩形截面长棒,由半导体锑化铟制成.棒中有平行于a边的电流I通过.该棒放在平行于c的外磁场B中,电流I所产生的磁场忽略不计.该电流的载流子为电子,在只有电场存在时,电子在半导体中的平均速度v=μE,(E为沿电流方向的匀强电场场强),其中μ为迁移率.分析 (1)霍尔元件中移动的是自由电子,根据电子所受洛伦兹力与电场力平衡,再结合电场强度与电势差之间的关系式E=$\frac{U}{d}$,联立即可求出b左右两表面上相对两点之间的电势差;
(2)根据电流微观表达式I=nqSv,结合已知条件v=μE,根据平行四边形定则,即可求出在棒中产生的总电场的大小,并用反三角函数表示其与a边的夹角α的大小.
(3)将E=$\frac{U}{d}$与电流的微观表达式I=nqSv以及题中已知:I=Imsinωt,B=Bmsin(ω+φ)联立,即可求出左右两边相对两点之间的电势差的直流分量的表达式;
解答 解:(1)设沿b方向的电场E1,
根据霍尔效应电场力与洛伦兹力平衡可得:eE1=evB
解得:E1=2.5V/m
根据电场强度与电势差的关系式可得:U=E1b
解得:U=2.5×10-2V
(2)设沿a方向的电流电场E2,
根据电流微观表达式:I=bcnev,
解得:v=$\frac{I}{bcne}$
根据已知:E2=$\frac{v}{μ}$,
代入数据解得:E2=3.2V/m
E=$\sqrt{{E}_{1}^{2}{+E}_{2}^{2}}$
E=$\sqrt{16.49}$V/m
α=arctan$\frac{{E}_{1}}{{E}_{2}}$=arctan$\frac{25}{32}$
(3)加上交变电流和交变磁场后,U′=E1b
U′=$\frac{IBb}{enbc}$=$\frac{{I}_{m}{B}_{m}}{enc}sinωt-sin(ωt+φ)$
U′=$\frac{{I}_{m}{B}_{m}}{enc}[\frac{1}{2}cos(2ωt+φ)+\frac{1}{2}cosφ]$
因此电势差的直流分量为:U′′=$\frac{{I}_{m}{B}_{m}}{2enc}cosφ$
答:(1)b左右两表面上相对两点之间的电势差为2.5×10-2V;
(2)在棒中产生的总电场的大小为$\sqrt{16.49}$V/m,总电场的方向与a边的夹角α的大小为arctan$\frac{25}{32}$;
(3)如果电流和磁场都是交变的,且分别为I=Imsinωt,B=Bmsin(ω+φ),左右两边相对两点之间的电势差的直流分量的表达式为U′′=$\frac{{I}_{m}{B}_{m}}{2enc}cosφ$;
点评 本题考查霍尔效应的应用,解题关键是要知道霍尔元件中移动的是自由电子,霍尔效应的平衡条件,即电子所受洛伦兹力与电场力平衡,还要知道电流的微观表达式I=nqSv并清楚式中每个物理量的意义.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中物理 来源: 题型:选择题
 如图所示,以9.8m/s的水平初速度v0抛出的物体,飞行一段时间后,垂直地撞在倾角θ为45°的斜面上,可知物体完成这段飞行的时间是( )
如图所示,以9.8m/s的水平初速度v0抛出的物体,飞行一段时间后,垂直地撞在倾角θ为45°的斜面上,可知物体完成这段飞行的时间是( )| A. | $\frac{{\sqrt{3}}}{3}$s | B. | 1s | C. | $\sqrt{3}$s | D. | 2s |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 如图所示,在xOy坐标平面内有垂直于坐标平面的圆形有界匀强磁场,磁场边界圆的圆心在x轴上O1处,O1点坐标为(R,0),磁场边界圆与y轴相切于坐标原点O.在y轴上P点(0,$\frac{\sqrt{2}}{2}$R)沿x轴正向以初速度v0射出一个质量为m,电荷量大小为q的带正电的粒子,粒子进入磁场后经磁场偏转,从圆心O1正下方的Q点射出磁场,不计粒子所受的重力,则( )
如图所示,在xOy坐标平面内有垂直于坐标平面的圆形有界匀强磁场,磁场边界圆的圆心在x轴上O1处,O1点坐标为(R,0),磁场边界圆与y轴相切于坐标原点O.在y轴上P点(0,$\frac{\sqrt{2}}{2}$R)沿x轴正向以初速度v0射出一个质量为m,电荷量大小为q的带正电的粒子,粒子进入磁场后经磁场偏转,从圆心O1正下方的Q点射出磁场,不计粒子所受的重力,则( )| A. | 磁场方向垂直于纸面向里 | |
| B. | 粒子在磁场中做圆周运动的半径为$\frac{\sqrt{2}}{2}$R | |
| C. | 匀强磁场的磁感应强度大小为B=$\frac{m{v}_{0}}{qR}$ | |
| D. | 粒子从Q点射出的方向与x轴负方向的夹角为45° |
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
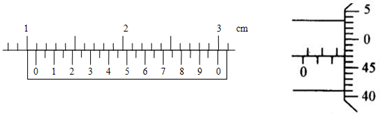 (1)图中游标卡尺的读数为10.90mm,螺旋测微器的读数为2.970mm.
(1)图中游标卡尺的读数为10.90mm,螺旋测微器的读数为2.970mm.查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 黑体辐射电磁波的强度按波长的分布只与黑体的温度有关 | |
| B. | 电子的衍射实验证实了德布罗意的物质波猜想 | |
| C. | 光的波长越长,光子的动量越大 | |
| D. | 光子具有波粒二象性,而实物粒子没有 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 如图所示,已知两个小物块A、B的质量分别为2m和m,随圆盘一起在水平面内做匀速圆周运动,它们轨道半径之比为rA:rB=1:2,小物块A、B与圆盘之间的动摩擦因数相同,则下列说法正确的是( )
如图所示,已知两个小物块A、B的质量分别为2m和m,随圆盘一起在水平面内做匀速圆周运动,它们轨道半径之比为rA:rB=1:2,小物块A、B与圆盘之间的动摩擦因数相同,则下列说法正确的是( )| A. | 小物块A所受摩擦力的方向与轨迹圆相切 | |
| B. | 小物块A、B所受向心力大小相等 | |
| C. | 小物块A、B的向心加速度大小之比为1:2 | |
| D. | 若逐渐增大圆盘角速度,小物块B首先相对圆盘滑动 |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
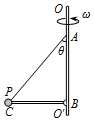 如图所示,杆OO′是竖直放置的转轴,水平轻杆BC的长为L,B端通过铰链与轴相连(它们之间无摩擦),C端固定小球P,细线AC的一端固定在轴上的A点、另一端连在小球P上.已知小球的质量为m,细线AC与轴的夹角θ,重力加速度为g.求:
如图所示,杆OO′是竖直放置的转轴,水平轻杆BC的长为L,B端通过铰链与轴相连(它们之间无摩擦),C端固定小球P,细线AC的一端固定在轴上的A点、另一端连在小球P上.已知小球的质量为m,细线AC与轴的夹角θ,重力加速度为g.求:查看答案和解析>>
科目:高中物理 来源: 题型:计算题

查看答案和解析>>
科目:高中物理 来源: 题型:计算题
 如图所示,电阻不计的平行金属导轨MN和OP水平放置,MO间接有阻值为R=0.5Ω的电阻,导轨相距为l=0.20m,其间有竖直向下的匀强磁场,磁感强度为B=0.50T,质量为m=0.1kg,电阻为r=0.5Ω的导体棒CD垂直于导轨放置,并接触良好.用平行于MN的恒力F=0.6N向右拉动CD.CD受恒定的摩擦阻力f=0.5N.求:
如图所示,电阻不计的平行金属导轨MN和OP水平放置,MO间接有阻值为R=0.5Ω的电阻,导轨相距为l=0.20m,其间有竖直向下的匀强磁场,磁感强度为B=0.50T,质量为m=0.1kg,电阻为r=0.5Ω的导体棒CD垂直于导轨放置,并接触良好.用平行于MN的恒力F=0.6N向右拉动CD.CD受恒定的摩擦阻力f=0.5N.求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com