
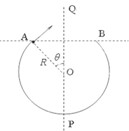
 如图所示,一个半径为R的光滑圆弧轨道APB竖直固定放置,PQ为其竖直对称轴,∠AOQ与∠BOQ都等于θ.现让一可看做质点的小球在轨道内侧运动,当其冲出A点后恰好可以从B点再进入轨道,所以此运动可以周而复始进行.已知小球质量为m,重力加速度为g,试求:
如图所示,一个半径为R的光滑圆弧轨道APB竖直固定放置,PQ为其竖直对称轴,∠AOQ与∠BOQ都等于θ.现让一可看做质点的小球在轨道内侧运动,当其冲出A点后恰好可以从B点再进入轨道,所以此运动可以周而复始进行.已知小球质量为m,重力加速度为g,试求: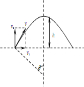
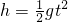 …⑤
…⑤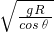 … ⑥
… ⑥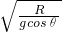 … ⑦
… ⑦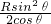 … ⑧
… ⑧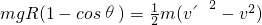 … ⑨
… ⑨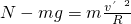 … ⑩
… ⑩ )
)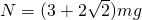 .
.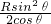 .
.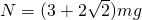 .
.

科目:高中物理 来源: 题型:
 如图所示,一个半径为R的光滑圆弧轨道APB竖直固定放置,PQ为其竖直对称轴,∠AOQ与∠BOQ都等于θ.现让一可看做质点的小球在轨道内侧运动,当其冲出A点后恰好可以从B点再进入轨道,所以此运动可以周而复始进行.已知小球质量为m,重力加速度为g,试求:
如图所示,一个半径为R的光滑圆弧轨道APB竖直固定放置,PQ为其竖直对称轴,∠AOQ与∠BOQ都等于θ.现让一可看做质点的小球在轨道内侧运动,当其冲出A点后恰好可以从B点再进入轨道,所以此运动可以周而复始进行.已知小球质量为m,重力加速度为g,试求:查看答案和解析>>
科目:高中物理 来源: 题型:
 (2005?浦东新区一模)如图所示,一个半径为R的半球形的碗固定在桌面上,碗口水平,O点为其球心,碗的内表面及碗口是光滑的.一根轻质细线跨在碗口上,线的两端分别系有小球A和B,当它们处于平衡状态时,小球A与O点的连线与水平线的夹角为60°.
(2005?浦东新区一模)如图所示,一个半径为R的半球形的碗固定在桌面上,碗口水平,O点为其球心,碗的内表面及碗口是光滑的.一根轻质细线跨在碗口上,线的两端分别系有小球A和B,当它们处于平衡状态时,小球A与O点的连线与水平线的夹角为60°.查看答案和解析>>
科目:高中物理 来源: 题型:
 (2012?山西二模)如图所示,一个半径为R、质量为M的半圆形光滑小碗,在它的边上
(2012?山西二模)如图所示,一个半径为R、质量为M的半圆形光滑小碗,在它的边上| 1 |
| 4 |
查看答案和解析>>
科目:高中物理 来源: 题型:
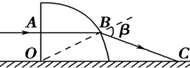 如图所示,一个半径为R的 透明圆柱体放置在水平面上,一束蓝光从A点沿水平方向射入圆柱体后经B点射出,最后射到水平面上的C点.已知OA=,该圆柱体对蓝光的折射率为,则:
如图所示,一个半径为R的 透明圆柱体放置在水平面上,一束蓝光从A点沿水平方向射入圆柱体后经B点射出,最后射到水平面上的C点.已知OA=,该圆柱体对蓝光的折射率为,则:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com