
 如图所示,水平固定轨道PM的左端P点与竖直粗糙半圆轨道平滑连接.一质量为m的滑块(可视为质点)从M点出发,向左冲上半圆轨道,并能恰好通过半圆轨道的最高点Q,已知半圆轨道的半径为R,M点和P点间的距离为2R,滑块与PM间的动摩擦因数μ=0.25,滑块通过P点时对半圆轨道的压力大小F=10mg(g为重力加速度大小),不计空气阻力,求:
如图所示,水平固定轨道PM的左端P点与竖直粗糙半圆轨道平滑连接.一质量为m的滑块(可视为质点)从M点出发,向左冲上半圆轨道,并能恰好通过半圆轨道的最高点Q,已知半圆轨道的半径为R,M点和P点间的距离为2R,滑块与PM间的动摩擦因数μ=0.25,滑块通过P点时对半圆轨道的压力大小F=10mg(g为重力加速度大小),不计空气阻力,求:分析 (1)根据牛顿第三定律求得滑块在P点受到的支持力,然后由牛顿第二定律求得速度,即可由动能定理求得在M点的速度;
(2)根据牛顿第二定律求得在Q的速度,然后由动能定理即可求得W;
(3)根据平抛运动规律直接求取水平位移x.
解答 解:(1)滑块通过P点时对半圆轨道的压力大小F=10mg,故由牛顿第三定律可得:滑块受到的支持力为10mg,那么,对滑块在P点应用牛顿第二定律可得:$10mg-mg=\frac{m{{v}_{P}}^{2}}{R}$,所以,${v}_{P}=3\sqrt{gR}$;
滑块从M到P的运动过程,只有摩擦力做功,故由动能定理可得:$-2μmgR=\frac{1}{2}m{{v}_{P}}^{2}-\frac{1}{2}m{{v}_{M}}^{2}$,所以,${v}_{M}=\sqrt{{{v}_{P}}^{2}+4μgR}=\sqrt{10gR}$;
(2)滑块能恰好通过半圆轨道的最高点Q,故对滑块在Q点应用牛顿第二定律可得:$mg=\frac{m{{v}_{Q}}^{2}}{R}$,所以,${v}_{Q}=\sqrt{gR}$;
滑块从P到Q的过程重力、阻力做功,故由动能定理可得:$-2mgR-W=\frac{1}{2}m{{v}_{Q}}^{2}-\frac{1}{2}m{{v}_{P}}^{2}=-4mgR$,所以,W=2mgR;
(3)滑块从Q点做平抛运动落回水平固定轨道,故由平抛运动规律可得:$2R=\frac{1}{2}g{t}^{2}$,$x={v}_{Q}t=\sqrt{gR}•\sqrt{\frac{4R}{g}}=2R$;
答:(1)滑块在M点的速度大小vM为$3\sqrt{gR}$;
(2)滑块从P点运动到Q点的过程中,克服阻力所做的功W为2mgR;
(3)滑块落回到水平固定轨道上的位置到P点的距离x为2R.
点评 经典力学问题一般先对物体进行受力分析,求得合外力及运动过程做功情况,然后根据牛顿定律、动能定理及几何关系求解.


科目:高中物理 来源: 题型:选择题
| A. | 宇航员受力平衡 | |
| B. | 宇航员所受重力等于需要的向心力 | |
| C. | 宇航员不受重力的作用 | |
| D. | 宇航员受重力且与地面所受重力相等 |
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 如图所示,质量分别为m和2m的A、B两物体叠放在劲度系数为k的竖直轻质弹簧上并保持静止,其中B带负电,电荷量大小为q,A始终不带电.现A、B所处空间加上场强大小为$\frac{mg}{q}$,方向竖直向下的匀强电场后,A、B开始运动并在运动了距离h时B与A分离.从开始运动到B和A刚分离的过程中,下列说法正确的是( )
如图所示,质量分别为m和2m的A、B两物体叠放在劲度系数为k的竖直轻质弹簧上并保持静止,其中B带负电,电荷量大小为q,A始终不带电.现A、B所处空间加上场强大小为$\frac{mg}{q}$,方向竖直向下的匀强电场后,A、B开始运动并在运动了距离h时B与A分离.从开始运动到B和A刚分离的过程中,下列说法正确的是( )| A. | B物体的动能一直增加 | B. | 两物体运动的距离h=$\frac{3mg}{k}$ | ||
| C. | B对A的压力一直减小 | D. | 物体B机械能的增加量为mgh |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
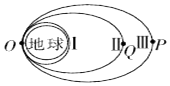 发射月球探测卫星要经过多次变轨.如图所示,I是某月球探测卫旱发射后的近地圆轨道.II、III是两次变轨后的转移椭圆轨道,O点是II、III轨道的近地点,Q、P分别是II、III轨道的远地点.则下列说法止确的是( )
发射月球探测卫星要经过多次变轨.如图所示,I是某月球探测卫旱发射后的近地圆轨道.II、III是两次变轨后的转移椭圆轨道,O点是II、III轨道的近地点,Q、P分别是II、III轨道的远地点.则下列说法止确的是( )| A. | 在二个轨道上,卫星在O点的速度相同 | |
| B. | 在三个轨道上,卫星在O点的加速度相同 | |
| C. | 卫星在Q点的机械能大于其在P点的机械能 | |
| D. | 卫星在Q点的机械能小于其在P点的机械能 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 所有行星绕太阳运动的轨道都是椭圆,太阳处在椭圆的一个焦点上 | |
| B. | 对于任意一个行星,其与太阳的连线在相等时间内扫过的面积相等 | |
| C. | 所有绕太阳运动的行星的轨道的半长轴的三次方跟公转周期的二次方的比值都相等 | |
| D. | 所有绕太阳运动的行星的轨道的半长轴的二次方跟公转周期的三次方的比值都相等 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
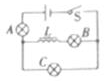 如图所示,三个不同的灯泡A、B、C和自感线L,串联后再与灯泡C并联,电源的内阻忽略不计,电路稳定后,三个灯泡均正常发光.已知自感线圈的系数很大,直流电阻可以忽略不计.则下列说法正确的是( )
如图所示,三个不同的灯泡A、B、C和自感线L,串联后再与灯泡C并联,电源的内阻忽略不计,电路稳定后,三个灯泡均正常发光.已知自感线圈的系数很大,直流电阻可以忽略不计.则下列说法正确的是( )| A. | 闭合开关S 到电路稳定前,灯泡A亮度减小 | |
| B. | 闭合开关S 到电路稳定前,灯泡C亮度增大 | |
| C. | 电路稳定后,断开开关S,灯泡A立刻熄灭 | |
| D. | 电路稳定后,断开开关S,灯泡B立刻熄灭 |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
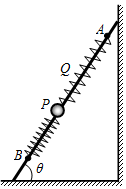 如图,固定直杆上套有一小球和两根轻弹簧,两根轻弹簧的一端与小球相连,另一端分别固定在杆上相距为2L的A、B两点.直杆与水平面的夹角为θ,小球质量为m,两根轻弹簧的原长均为L、劲度系数均为$\frac{3mgsinθ}{L}$,g为重力加速度.
如图,固定直杆上套有一小球和两根轻弹簧,两根轻弹簧的一端与小球相连,另一端分别固定在杆上相距为2L的A、B两点.直杆与水平面的夹角为θ,小球质量为m,两根轻弹簧的原长均为L、劲度系数均为$\frac{3mgsinθ}{L}$,g为重力加速度.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com