
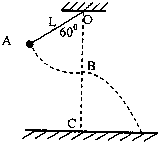
 如图所示,初态细线OA与竖直方向OB夹角为60°,让摆球从图中A位置由静止开始下摆,正好到最低点B位置时线被拉断,设摆线长L=1.6m,悬点O与地面的竖直高度OC=6.6m,不计空气阻力,求摆球着地时距c多远?(g取10m/s2)
如图所示,初态细线OA与竖直方向OB夹角为60°,让摆球从图中A位置由静止开始下摆,正好到最低点B位置时线被拉断,设摆线长L=1.6m,悬点O与地面的竖直高度OC=6.6m,不计空气阻力,求摆球着地时距c多远?(g取10m/s2)| 1 |
| 2 |
| 2gL(1-cos60°) |
| 2×10×1.6×0.5 |
|
|


 星级口算天天练系列答案
星级口算天天练系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com