
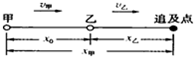
 解:(1)设甲经过时间t追上乙,则有:
解:(1)设甲经过时间t追上乙,则有: a甲t2,x乙=v乙t
a甲t2,x乙=v乙t a甲t2=x0+v乙t,
a甲t2=x0+v乙t,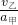 =
= s=l0 s.
s=l0 s. a甲t12=200m+5×10m-
a甲t12=200m+5×10m- ×0.5×102m=225m
×0.5×102m=225m

 口算能手系列答案
口算能手系列答案科目:高中物理 来源: 题型:
查看答案和解析>>
科目:高中物理 来源: 题型:
查看答案和解析>>
科目:高中物理 来源: 题型:
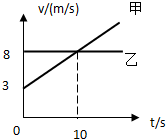 在平直公路上有甲、乙两辆车在同一地点向同一方向运动,如图:速度图象,求:
在平直公路上有甲、乙两辆车在同一地点向同一方向运动,如图:速度图象,求:. | v |
查看答案和解析>>
科目:高中物理 来源: 题型:
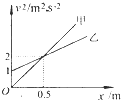 在平直公路上有甲、乙两辆汽车同时从同一位置沿着同一方向做匀加速直线运动,它们速度的平方随位移变化的图象如图所示,则( )
在平直公路上有甲、乙两辆汽车同时从同一位置沿着同一方向做匀加速直线运动,它们速度的平方随位移变化的图象如图所示,则( )| A、甲车的加速度比乙车的加速度小 | B、在x=0.5m处甲乙两车相遇 | C、在x=1m处甲乙两车相遇 | D、在t=2s末甲乙两车相遇 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com