
 »зЌЉ£ЃЋЃ∆љ√жƒЏ”–“ї°∞°ѕ°±–Ќєвїђљр фµЉємCOD£ђµз„и≤їЉ∆£ђ°ѕCOD=45°г£Ѓ„гєї≥§÷±µЉће∞фЄй‘ЏµЉєм…ѕ£ђµ•ќї≥§ґ»µƒµз„иќ™r=0.5¶Є£ђµЉће∞фіє÷±OD£Ѓњ’Љдіж‘Џіє÷±”ЏµЉєм∆љ√жµƒі≈≥°£ђ“‘Oµгќ™‘≠µг—Ў0DЈљѕтљ®ЅҐ„ш±к÷б£ђµЉємЉдx£Њ0“ї≤аіж‘Џ—ЎxЈљѕтЊщ‘»‘ціуµƒќ»Їгі≈≥°£ђ±дїѓ¬ ќ™0.5T/m£ђOµгі≈Є–”¶«њґ»B0=1T£Ѓ‘ЏЌвЅ¶„ч”√ѕ¬£ђ∞ф“‘“їґ®µƒ≥хЋўґ»ѕт”“„ц÷±ѕя‘Ћґѓ£ђ‘Ћґѓ ±їЎ¬Ј÷–µƒµзЅч«њґ»±£≥÷≤ї±д£Ѓ“—÷™‘ЋґѓµљЌЉ÷–x1=1mќї÷√ ±£ђЋўґ»іу–°v1=2m/s£ђ‘тїЎ¬Ј÷–µƒµзЅч«њґ»іу–°ќ™6A£ђі”x1=1mќї÷√‘ўѕт”“‘Ћґѓ1mµƒєэ≥ћ÷–£ђЌ®єэµЉће∞фµƒµзЅњќ™3.5C£Ѓ
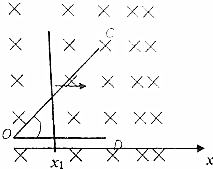
»зЌЉ£ЃЋЃ∆љ√жƒЏ”–“ї°∞°ѕ°±–Ќєвїђљр фµЉємCOD£ђµз„и≤їЉ∆£ђ°ѕCOD=45°г£Ѓ„гєї≥§÷±µЉће∞фЄй‘ЏµЉєм…ѕ£ђµ•ќї≥§ґ»µƒµз„иќ™r=0.5¶Є£ђµЉће∞фіє÷±OD£Ѓњ’Љдіж‘Џіє÷±”ЏµЉєм∆љ√жµƒі≈≥°£ђ“‘Oµгќ™‘≠µг—Ў0DЈљѕтљ®ЅҐ„ш±к÷б£ђµЉємЉдx£Њ0“ї≤аіж‘Џ—ЎxЈљѕтЊщ‘»‘ціуµƒќ»Їгі≈≥°£ђ±дїѓ¬ ќ™0.5T/m£ђOµгі≈Є–”¶«њґ»B0=1T£Ѓ‘ЏЌвЅ¶„ч”√ѕ¬£ђ∞ф“‘“їґ®µƒ≥хЋўґ»ѕт”“„ц÷±ѕя‘Ћґѓ£ђ‘Ћґѓ ±їЎ¬Ј÷–µƒµзЅч«њґ»±£≥÷≤ї±д£Ѓ“—÷™‘ЋґѓµљЌЉ÷–x1=1mќї÷√ ±£ђЋўґ»іу–°v1=2m/s£ђ‘тїЎ¬Ј÷–µƒµзЅч«њґ»іу–°ќ™6A£ђі”x1=1mќї÷√‘ўѕт”“‘Ћґѓ1mµƒєэ≥ћ÷–£ђЌ®єэµЉће∞фµƒµзЅњќ™3.5C£Ѓ Ј÷ќц ѕ»ЄщЊЁћв“в«у≥цx1=1mќї÷√і≈Є–”¶«њґ»ЇЌµЉће∞ф”––Іµƒ«–Єо≥§ґ»£ђ‘ў”…E=BLv«у≥цЄ–”¶µзґѓ ∆£ђ‘ў”…≈ЈƒЈґ®¬…«у≥цїЎ¬Ј÷–µƒµзЅч«њґ»£Ѓ
µЉће∞фѕт”“‘Ћґѓµƒєэ≥ћ÷–£ђBЊщ‘»‘ціу£ђљбЇѕB-xЌЉѕуµƒ√жїэ«у≥ці≈Ќ®Ѕњµƒ±дїѓЅњ°ч¶µ£ђЄщЊЁq=$\frac{°ч¶µ}{R}$«уЌ®єэµЉће∞фµƒµзЅњ£Ѓ
љвір љв£Ї”…ћвњ…µ√£ђx1=1mќї÷√і≈Є–”¶«њґ» B1=B0+0.5x1=1+0.5=1.5T
µЉће∞ф”––Іµƒ«–Єо≥§ґ» L1=x1=1m
‘тµЉће∞ф≤ъ…ъµƒЄ–”¶µзґѓ ∆ E=B1L1v1=1.5°Ѕ1°Ѕ2=3V
їЎ¬Ј÷–µƒµз„и R=rx1=0.5¶Є
”…≈ЈƒЈґ®¬…µ√£ђїЎ¬Ј÷–µƒµзЅч«њґ»іу–° I=$\frac{E}{R}$=6A
…и“∆ґѓµљxќї÷√£®1£Љx£Љ2£©
‘ЏЉЂґћ ±Љд°чtƒЏ≤ъ…ъµƒµзЅњ°чq=I°чt
іЋ ±Bµƒіу–°ќ™ Bx=B0+0.5x
l=x£ђv1=2m/s£ђµз„иRµƒіу–° 0.5x
µЉће∞ф≤ъ…ъµƒЄ–”¶µзґѓ ∆ќ™ E=Blv=£®x+0.5x£©xv
Є–”¶µзЅч I=$\frac{E}{R}$=$\frac{£®1+0.5x£©xv}{0.5x}$=£®2+x£©v
‘т°чq=£®2+x£©v°чt
°чt=$\frac{°чx}{v}$
µ√°чq=£®2+x£©v•$\frac{°чx}{v}$=£®2+x£©°чx
є q=£®$\frac{1}{2}{x}^{2}$+2x£©|${\;}_{1}^{2}$=3.5C
є ір∞Єќ™£Ї6£ђ3.5£Ѓ
µг∆ј љвЊц±ЊћвµƒєЎЉь «ЄщЊЁЈ®ј≠µЏґ®¬…°Ґ≈ЈƒЈґ®¬…µ√µљµзЅњ”лxµƒєЎѕµ љ£ђ≤…”√їэЈ÷Ј®«уµзЅњ£Ѓ


 ‘ƒґЅњм≥µѕµЅ–ір∞Є
‘ƒґЅњм≥µѕµЅ–ір∞Є
| ƒкЉґ | Єя÷–њќ≥ћ | ƒкЉґ | ≥х÷–њќ≥ћ |
| Єя“ї | Єя“ї√вЈ—њќ≥ћЌ∆Љц£° | ≥х“ї | ≥х“ї√вЈ—њќ≥ћЌ∆Љц£° |
| Єяґю | Єяґю√вЈ—њќ≥ћЌ∆Љц£° | ≥хґю | ≥хґю√вЈ—њќ≥ћЌ∆Љц£° |
| Єя»э | Єя»э√вЈ—њќ≥ћЌ∆Љц£° | ≥х»э | ≥х»э√вЈ—њќ≥ћЌ∆Љц£° |
њ∆ƒњ£ЇЄя÷–ќпјн јі‘і£Ї ћв–Ќ£Їљвірћв
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£ЇЄя÷–ќпјн јі‘і£Ї ћв–Ќ£Їћоњ’ћв
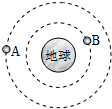 »зЌЉЋщ Њ£ђ»Ћ‘мќј–«A°ҐB‘ЏЌђ“ї∆љ√жƒЏ»∆µЎ«т„ц‘»Ћў‘≤÷№‘Ћґѓ£Ѓ‘тќј–«AµƒѕяЋўґ»–°”Џќј–«BµƒѕяЋўґ»£ђќј–«AµƒЉ”Ћўґ»–°”Џќј–«BµƒЉ”Ћўґ»£®—°ћо°∞іу”Џ°±°Ґ°∞–°”Џ°±їт°∞µ»”Џ°±£©£Ѓ
»зЌЉЋщ Њ£ђ»Ћ‘мќј–«A°ҐB‘ЏЌђ“ї∆љ√жƒЏ»∆µЎ«т„ц‘»Ћў‘≤÷№‘Ћґѓ£Ѓ‘тќј–«AµƒѕяЋўґ»–°”Џќј–«BµƒѕяЋўґ»£ђќј–«AµƒЉ”Ћўґ»–°”Џќј–«BµƒЉ”Ћўґ»£®—°ћо°∞іу”Џ°±°Ґ°∞–°”Џ°±їт°∞µ»”Џ°±£©£Ѓ≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£ЇЄя÷–ќпјн јі‘і£Ї ћв–Ќ£Ї—°‘сћв
 ∆ы≥µ‘Џє∞«≈…ѕ‘»Ћў¬ –– ї£ђµ±∆ы≥µ”…є∞«≈µƒ„оЄяµгA–– їµљ„оµЌµгBµƒєэ≥ћ÷–£ђѕ¬Ѕ–ЋµЈ®≤ї’э»Јµƒ «£®°°°°£©
∆ы≥µ‘Џє∞«≈…ѕ‘»Ћў¬ –– ї£ђµ±∆ы≥µ”…є∞«≈µƒ„оЄяµгA–– їµљ„оµЌµгBµƒєэ≥ћ÷–£ђѕ¬Ѕ–ЋµЈ®≤ї’э»Јµƒ «£®°°°°£©| A£Ѓ | ÷І≥÷Ѕ¶≤ї„цє¶ | B£Ѓ | ÷ЎЅ¶≤ї„цє¶ | C£Ѓ | ƒ¶≤ЅЅ¶„чЄЇє¶ | D£Ѓ | «£“эЅ¶„ц’эє¶ |
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£ЇЄя÷–ќпјн јі‘і£Ї ћв–Ќ£Ї—°‘сћв
| A£Ѓ | C=4¶–?$\frac{{R}_{A}+{R}_{B}}{\sqrt{{R}_{A}{R}_{B}}}$ | B£Ѓ | C=4¶–?$\frac{{R}_{B}-{R}_{A}}{\sqrt{{R}_{A}{R}_{B}}}$ | C£Ѓ | C=4¶–?$\frac{{R}_{B}{R}_{A}}{{R}_{B}-{R}_{A}}$ | D£Ѓ | C=4¶–?$\frac{{R}_{B}{R}_{A}}{{R}_{B}+{R}_{A}}$ |
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£ЇЄя÷–ќпјн јі‘і£Ї ћв–Ќ£Ї µ—йћв

≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£ЇЄя÷–ќпјн јі‘і£Ї ћв–Ќ£Ї—°‘сћв
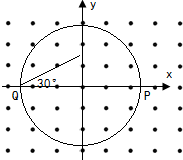 »зЌЉЋщ Њ£ђ‘Џ÷±љ«„шЉ ѕµx0yƒЏ£ђ“‘‘≠µг0ќ™‘≤–ƒ£ђ∞лЊґќ™Rµƒ‘≤–ќ«ш”тƒЏіж‘Џ„≈іє÷±÷љ√жѕтЌвµƒ‘»«њі≈≥°£ђ“їЄЇµз„”і”Pµг£®R£ђ0£©—Ўx÷бЄЇЈљѕт“‘Ћў¬ v…д»лі≈≥°Їу£ђ‘Џі≈≥°÷–‘Ћґѓµƒ ±Љдќ™t1£ђ“ї’эµз„”і”Qµг£®-R£ђ0£©—Ў„≈”лx÷б’эѕт≥…30°гµƒЈљѕт“‘Ћў¬ 2v…д»лі≈≥°Їу£ђ«°Ї√і”PµгЈ…≥ці≈≥°£ђ‘Џі≈≥°÷–‘Ћґѓµƒ ±Љдќ™t2£ђЇц¬‘Ѕљµз„”÷ЎЅ¶Љ∞ѕаї•„ч”√Ѕ¶£ђ‘тt1£Їt2ќ™£®°°°°£©
»зЌЉЋщ Њ£ђ‘Џ÷±љ«„шЉ ѕµx0yƒЏ£ђ“‘‘≠µг0ќ™‘≤–ƒ£ђ∞лЊґќ™Rµƒ‘≤–ќ«ш”тƒЏіж‘Џ„≈іє÷±÷љ√жѕтЌвµƒ‘»«њі≈≥°£ђ“їЄЇµз„”і”Pµг£®R£ђ0£©—Ўx÷бЄЇЈљѕт“‘Ћў¬ v…д»лі≈≥°Їу£ђ‘Џі≈≥°÷–‘Ћґѓµƒ ±Љдќ™t1£ђ“ї’эµз„”і”Qµг£®-R£ђ0£©—Ў„≈”лx÷б’эѕт≥…30°гµƒЈљѕт“‘Ћў¬ 2v…д»лі≈≥°Їу£ђ«°Ї√і”PµгЈ…≥ці≈≥°£ђ‘Џі≈≥°÷–‘Ћґѓµƒ ±Љдќ™t2£ђЇц¬‘Ѕљµз„”÷ЎЅ¶Љ∞ѕаї•„ч”√Ѕ¶£ђ‘тt1£Їt2ќ™£®°°°°£©| A£Ѓ | 2£Ї3 | B£Ѓ | 3£Ї2 | C£Ѓ | 3£Ї1 | D£Ѓ | 1£Ї2 |
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£ЇЄя÷–ќпјн јі‘і£Ї ћв–Ќ£Ї—°‘сћв
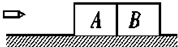 »зЌЉЋщ Њ£ђ‘ЏєвїђЋЃ∆љ√ж…ѕЊ≤÷єЈ≈„≈ЅљЄцѕаї•љ”і•µƒƒЊњйA°ҐB£ђ÷ ЅњЈ÷±рќ™m 1ЇЌm 2£ђљс”–“ї„”µѓЋЃ∆љі©єэЅљƒЊњй£Ѓ…и„”µѓі©єэƒЊњйA°ҐBµƒ ±ЉдЈ÷±рќ™t1ЇЌt2£ђƒЊњйґ‘„”µѓµƒ„иЅ¶Їгќ™f£ђ‘т„”µѓі©єэЅљƒЊњйЇу£ђƒЊњйA°ҐBµƒЋўґ»іу–°Ј÷±р «£®°°°°£©
»зЌЉЋщ Њ£ђ‘ЏєвїђЋЃ∆љ√ж…ѕЊ≤÷єЈ≈„≈ЅљЄцѕаї•љ”і•µƒƒЊњйA°ҐB£ђ÷ ЅњЈ÷±рќ™m 1ЇЌm 2£ђљс”–“ї„”µѓЋЃ∆љі©єэЅљƒЊњй£Ѓ…и„”µѓі©єэƒЊњйA°ҐBµƒ ±ЉдЈ÷±рќ™t1ЇЌt2£ђƒЊњйґ‘„”µѓµƒ„иЅ¶Їгќ™f£ђ‘т„”µѓі©єэЅљƒЊњйЇу£ђƒЊњйA°ҐBµƒЋўґ»іу–°Ј÷±р «£®°°°°£©| A£Ѓ | $\frac{f{t}_{1}}{{m}_{1}}$ $\frac{f{t}_{1}}{{m}_{1}+{m}_{2}}$ | |
| B£Ѓ | $\frac{f{t}_{1}}{{m}_{1}+{m}_{2}}$ $\frac{f{t}_{1}}{{m}_{1}+{m}_{2}}$+$\frac{f{t}_{2}}{{m}_{2}}$ | |
| C£Ѓ | $\frac{f{t}_{1}}{{m}_{1}}$ $\frac{f£®{t}_{1}+{t}_{2}£©}{{m}_{1}+{m}_{2}}$ | |
| D£Ѓ | $\frac{f£®{t}_{1}+{t}_{2}£©}{{m}_{1}}$ $\frac{f£®{t}_{1}+{t}_{2}£©}{{m}_{1}+{m}_{2}}$ |
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£ЇЄя÷–ќпјн јі‘і£Ї ћв–Ќ£Ї—°‘сћв
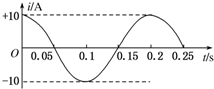
| A£Ѓ | ÷№∆Џ «0.2 s£ђµзЅчµƒЈе÷µ «10$\sqrt{2}$A | B£Ѓ | ÷№∆Џ «0.25 s£ђµзЅчµƒЈе÷µ «10 A | ||
| C£Ѓ | ∆µ¬ «5 Hz£ђµзЅчµƒ”––І÷µ «10 A | D£Ѓ | ∆µ¬ «5 Hz£ђµзЅчµƒ”––І÷µ «5$\sqrt{2}$A |
≤йњіір∞ЄЇЌљвќц>>
єъЉ —І–£”≈—° - ЅЈѕ∞≤бЅ–±н - ‘ћвЅ–±н
Їю±± °ї•Ѕ™Ќшќ•Ј®ЇЌ≤їЅЉ–≈ѕҐЊў±®∆љћ® | Ќш…ѕ”–Ї¶–≈ѕҐЊў±®„®«ш | µз–≈’©∆≠Њў±®„®«ш | …жјъ Ј–йќё÷ч“е”–Ї¶–≈ѕҐЊў±®„®«ш | …ж∆у«÷»®Њў±®„®«ш
ќ•Ј®ЇЌ≤їЅЉ–≈ѕҐЊў±®µзї∞£Ї027-86699610 Њў±®” ѕд£Ї58377363@163.com