练习册

  • 练习册
  • 试题
    精英家教网 > 高中物理 > 题目详情
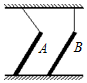
    9．如图所示，A、B两均匀直杆上端分别用细线悬挂于天花板上，下端搁在水平地面上，处于静止状态，悬挂A杆的绳倾斜，悬挂B杆的绳恰好竖直，则下列说法中正确的有（　　）
    A．地面对A的作用力的方向竖直向上B．A有向左运动的趋势
    C．地面对B的支持力可能为零D．地面对B的摩擦力方向向右

    分析 分别以A和B为研究对象进行受力分析，根据共点力的平衡条件分析A和B是否受到地面的摩擦力作用．

    解答 解：AB、物体A受重力，绳子向左上方的拉力，A有向左运动的趋势，地面对A杆有支持力和向右的静摩擦力，所以地面对A的作用力的方向斜向右上方，不是竖直向上，所以A错误、B正确；
    CD、物体B受重力、绳子竖直向上的拉力和地面的支持力，无静摩擦力，若有，水平方向不能平衡，故CD错误．
    故选：B．

    点评 受力分析是解决力学问题的基础，要能结合产生条件、作用效果分析，本题是将拉力分解后根据平衡条件判断有无静摩擦力．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中物理 来源： 题型：选择题

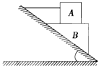    19．如图，在斜面上木块 A 与 B 的接触面是水平的，绳子呈水平状态，两木块均保持静止．则 关于木块 A 和木块 B 受力个数不可能的（　　）
    A．2 个和 4 个B．3 个和 4 个C．4 个和 4 个D．4 个和 5 个

    查看答案和解析>>

    科目：高中物理 来源： 题型：计算题

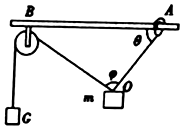    20．如图所示，在质量为m=1kg的重物上系着两条细绳，细绳OA的另一端连着圆环，圆环套在水平的棒上可以滑动，环与棒间的动摩擦因数μ=0.74，另有一条细绳，其一端跨过定滑轮挂一重物，定滑轮固定在水平棒上的B点，当细绳的端点挂上质量为0.6kg的重物G时，圆环将要开始滑动，此时两条细绳的夹角φ=90°，（设最大静摩擦力等于滑动摩擦，g取10m/s2）试问：
    （1）此时细绳OA的拉力是多少？
    （2）圆环的质量是多少？

    查看答案和解析>>

    科目：高中物理 来源： 题型：选择题

    17．下列说法中正确的是（　　）
    A．单位m、kg、s、N是一组属于国际单位制的基本单位
    B．牛顿第一定律、牛顿第二定律都可以通过实验来证明
    C．一对作用力和反作用力总是同时存在、同时变化
    D．做曲线运动的质点，加速度可以为零

    查看答案和解析>>

    科目：高中物理 来源： 题型：选择题

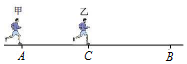    4．如图所示，甲从A地由静止匀加速跑向B地，当甲前进距离为1m时，乙从距A地5m处的C点由静止出发，乙的加速度与甲的加速度相同，最后二人同时到达B地，则A、B两地距离为（　　）
    A．6mB．9mC．12mD．15m

    查看答案和解析>>

    科目：高中物理 来源： 题型：多选题

    14．关于惯性，下列说法中正确的是（　　）
    A．运动员在掷标枪时的助跑是为了利用惯性
    B．运动员在跳远时的助跑是为了增大起跳时的惯性
    C．战斗机在空战时，甩掉副油箱是为了减小惯性，提高飞行的灵活性
    D．踢出去的足球由于受到惯性作用仍然能够在草地上滚动

    查看答案和解析>>

    科目：高中物理 来源： 题型：选择题

    1．关于牛顿第一定律，下面说法中正确的是（　　）
    A．牛顿第一定律反映了物体受外力作用时物体的运动规律．
    B．牛顿第一定律就是惯性．
    C．不受外力作用时，物体运动状态保持不变是由于物体具有惯性．
    D．运动的物体状态发生变化时，物体可能不受到外力的作用．

    查看答案和解析>>

    科目：高中物理 来源： 题型：选择题

    18．下列关于平均速度和瞬时速度的说法中正确的是（　　）
    A．做匀变速运动的物体在相同时间间隔里的平均速度是相同的
    B．瞬时速度就是运动的物体在一段较短时间内的平均速度
    C．某物体在某段时间里的瞬时速度都为零，则该物体在这段时间内静止
    D．平均速度就是初末时刻瞬时速度的平均值

    查看答案和解析>>

    科目：高中物理 来源： 题型：实验题

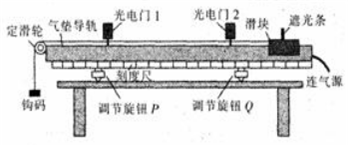    13．某同学利用如图所示的气垫导轨装置验证机械能守恒定律．在气垫导轨上安装了相同的两光电门1、2，滑块上固定一遮光条，滑块用细线绕过轻质定滑轮与钩码相连．
    （1）实验时要调整气垫导轨水平．不挂钩码和细线，接通气源，如果滑块能在气垫导轨上静止，或做匀速运动，或滑块经两个光电门的时间相等，则表示气垫导轨已调整至水平状态．
    （2）不挂钩码和细线，接通气源，滑块从轨道右端向左运动的过程中，发现滑块通过光电门1的时间小于通过光电门2的时间．实施下列措施能够让导轨水平的是A．
    A．调节P使轨道左端升高一些
    B．调节Q使轨道右端升高一些
    C．调节光电门之间距离小一些
    D．遮光条的宽度应适当大一些
    E．气源的供气量适当增大一些
    （3）实验时，测出光电门1、2间的距离L，遮光条的宽度d，滑块和遮光条的总质量M，钩码质量m．由数字计时器读出遮光条通过光电门1、2的时间t1、t2，则滑块和钩码组成的系统机械能守恒成立的表达式是$mgL=\frac{1}{2}（M+m）（\frac{d}{{t}_{1}^{\;}}）_{\;}^{2}-\frac{1}{2}（M+m）（\frac{d}{{t}_{2}^{\;}}）_{\;}^{2}$=$\frac{1}{2}（M+m）{d}_{\;}^{2}（\frac{1}{{t}_{1}^{2}}-\frac{1}{{t}_{2}^{2}}）$．

    查看答案和解析>>

    同步练习册答案